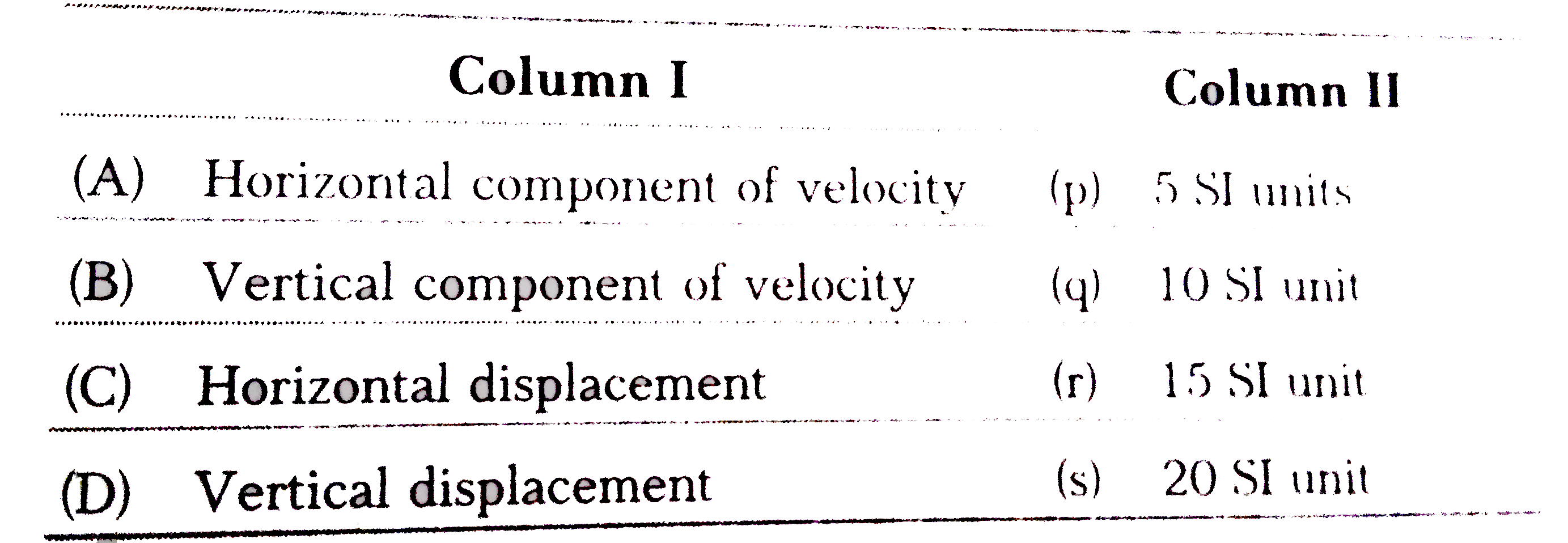Home
Class 11
PHYSICS
A particle is projected horizontally for...

A particle is projected horizontally form a tower with velocity `10 ms^(-1)`. Taking `g = 10 ms^(-2)`. Match the following two columns at time t = 1s.

Text Solution

Verified by Experts

The correct Answer is:
`A rarr q,B rarr q,C rarr q,D rarr p`
In horizontal projectile motion, Horizontal component of velocity `u_(x) = u = 10 ms^(-1)`
Vertical component of velocity `u_(y) = g t = 10 xx 1 = 10 ms^(-1)`
Horizontal displacement `= u xx t = 10 xx (1) = 10m`
Vertical displacement `= (1)/(2)g t^(2) = (1)/(2) xx 10 xx (1)^(2) = 5m`
Promotional Banner

Topper's Solved these Questions

  • MOTION

    DC PANDEY ENGLISH|Exercise C. Medical entrances gallery|1 Videos

  • MOTION

    DC PANDEY ENGLISH|Exercise Medical entrances gallery|19 Videos

  • MOTION

    DC PANDEY ENGLISH|Exercise Medical entrance|12 Videos

  • MEASUREMENT AND ERRORS

    DC PANDEY ENGLISH|Exercise Subjective|19 Videos

  • MOTION IN A PLANE

    DC PANDEY ENGLISH|Exercise (C )Medical entrances gallery|32 Videos

Similar Questions

Explore conceptually related problems

A stone is projected from the top of a tower with velocity 20ms^(-1) making an angle 30^(@) with the horizontal. If the total time of flight is 5s and g=10ms^(-2)

A particle of mass 50 g is projected horizontally from the top of a tower of height 50 m with a velocity 20m//s . If g=10m//s^(2) , then find the :-

A particle is projected at an angle theta =30^@ with the horizontal, with a velocity of 10ms^(-1) . Then

A stone is projected horizontally with a velocity 9.8 ms ^(-1) from a tower of height 100 m. Its velocity one second after projection is (g = 9.8 ms ^(-2)).

A particle is projected form ground with velocity u ar angle theta from horizontal. Match the following two columns.

A body is projected horizontally from a height of 78.4 m with a velocity 10 ms^(-1) . Its velocity after 3 seconds is [g = 10 ms^(-2) ] (Take direction of projection on veci and vertically upward direction on j)

A stone is projected vertically up from the ground with velocity 40 ms^(-1) . The interval of time between the two instants at which the stone is at a height of 60 m above the ground is (g = 10 "ms"^(-2))

A body is projected horizontally from the top of a tower with a velocity of 30 m/s. The velocity of the body 4 seconds after projection is (g = 10ms^(-2) )

A bullet is projected upwards from the top of a tower of height 90 m with the velocity 30 ms^(-1) making an angle 30^(@) with the horizontal. Find the time taken by it to reach the ground is (g=10 ms^(-2))

A body is projected at angle 30° to horizontal with a velocity 50 ms^(-1) . Its time of flight is (g=10 m//s^2 )