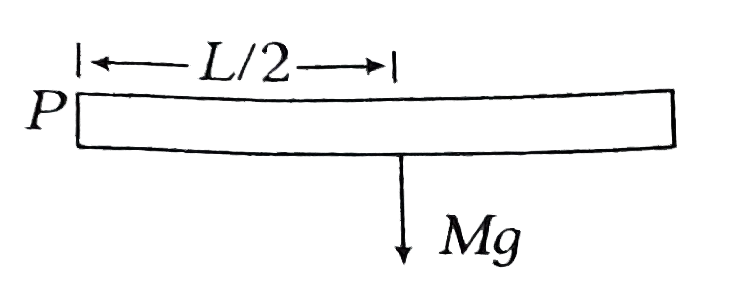
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-ROTATION-(C) Chapter Exercises
- Two bodies have their moments of inertia I and 2I, respectively about ...
Text Solution
|
- A body having a moment of inertia about its axis of rotation equal to ...
Text Solution
|
- A uniform solid spherical ball is rolling down a smooth inclined plane...
Text Solution
|
- A rod PQ of mass M and length L is hinged at end P. The rod is kept ho...
Text Solution
|
- A small object of uniform density rolls up a curved surface with an in...
Text Solution
|
- The conservation of angular momentum demands that
Text Solution
|
- The moment of inertia (I) and the angular momentum (L) are related by ...
Text Solution
|
- The moment of ineria (I) of a sphere of radius R and mass M is given b...
Text Solution
|
- A particle mass m is attched to a thin uniform rod of length a at a di...
Text Solution
|
- A particle moving in a circular path has an angular momentum of L. If ...
Text Solution
|
- The torque of a force F = 2 hat(i) - 3 hat(j) +5 hat(k) acting at a po...
Text Solution
|
- Moment of inertia of a ring of radius R about a diametric axis is 25 "...
Text Solution
|
- A wheel having moment of inertia 2 "kg-m"^(2) about its vertical axis,...
Text Solution
|
- What is the moment of inertia of solid sphere of density rho and radiu...
Text Solution
|
- The radius of gyration of a body depends upon
Text Solution
|
- Two discs have same mass and thickness. Their materials are of densiti...
Text Solution
|
- If a disc starting from rest acquires an angular velocity of 240 "rev ...
Text Solution
|
- A thin hollow sphere of mass m is completely filled with a liquid of m...
Text Solution
|
- The moment of inertia of a circular loop of radius R, at a distance of...
Text Solution
|
- A rod of length L is composed of a uniform length 1/2 L of wood mass i...
Text Solution
|