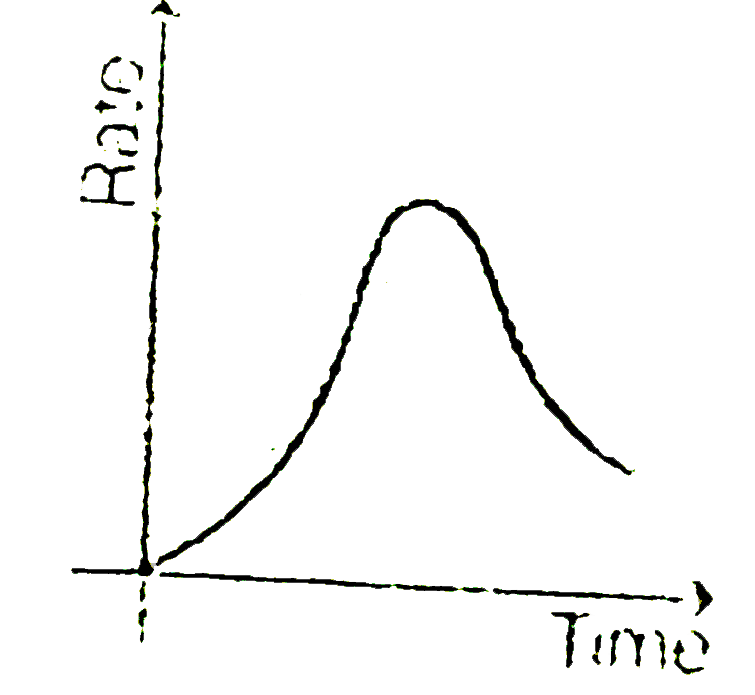
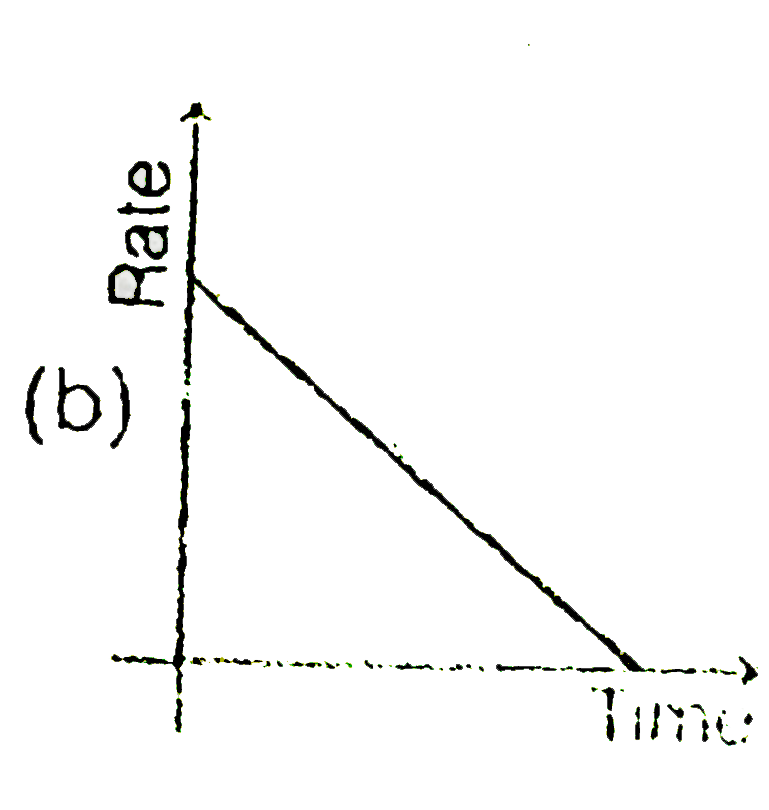
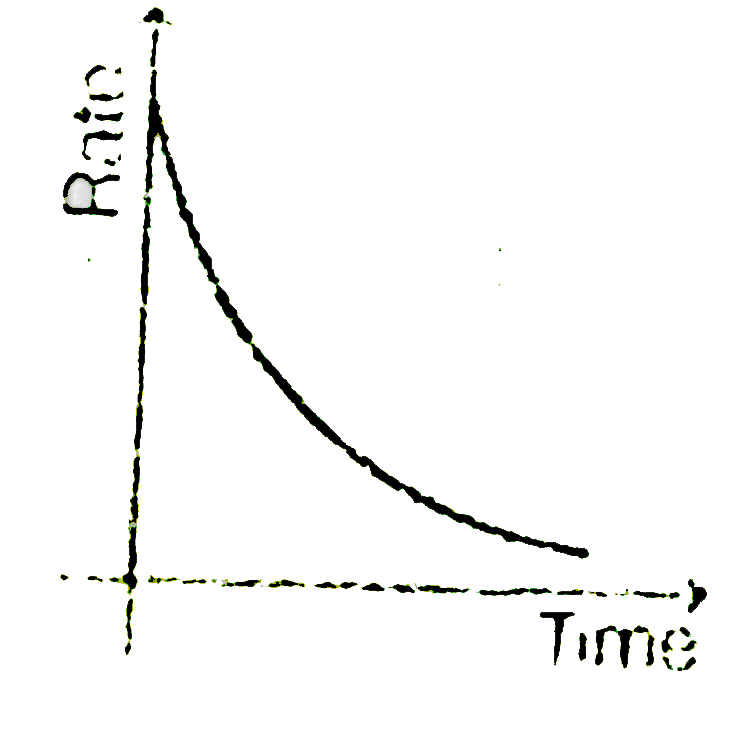
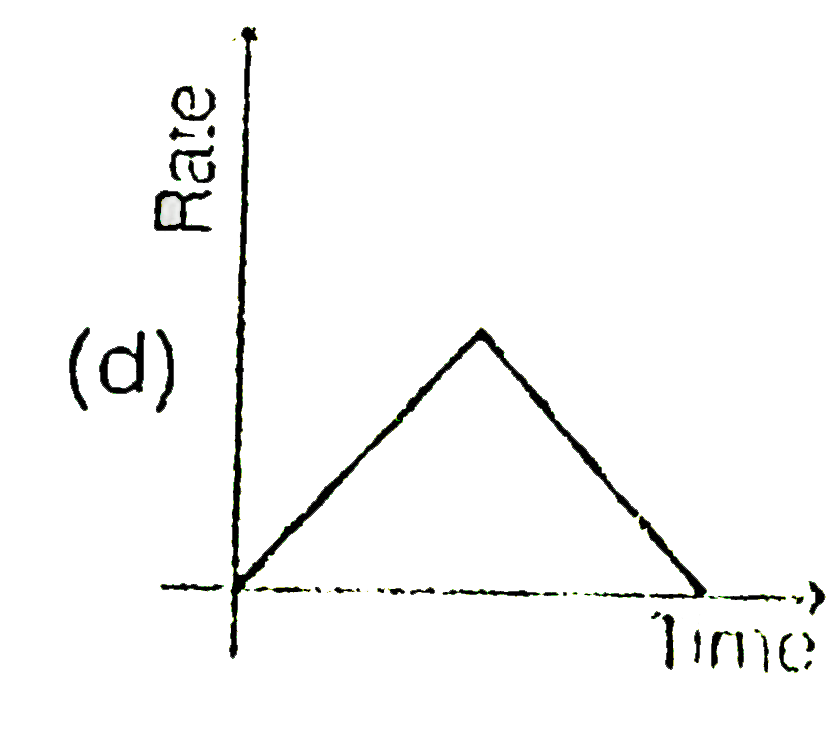
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In an LR circuit connected to a battery, the rate at which energy is s...
Text Solution
|
- In an LR circuit connected to a battery, the rate at which energy is s...
Text Solution
|
- A simple LR circuit is connected to a battery at time t = 0 . The ener...
Text Solution
|
- A series RLC circuit is connected to an ac generator. The instant at w...
Text Solution
|
- Consider a circuit consists of resistors, inductor, battery and a swit...
Text Solution
|
- The rate of decay (R ) of nuclei in a radioactive sample is plotted ag...
Text Solution
|
- The time constant of an LR circuit respresents the time in which the c...
Text Solution
|
- Rate of increment of energy in an inductor with time in series RL circ...
Text Solution
|
- The rate of decay (R ) of nuclei in a radioactive sample is plotted ag...
Text Solution
|