Two parallel long straight conductors lie on a smooth horizontal surface. Two other parallel conductor rest on them at right angles so as from B exits vertical. A uniform magnetic field B exists a vertical direction. Now all the four conductors stock moving outwards with a constant velocity v. The induced emf e and induced current i will vary wide time t as
Two parallel long straight conductors lie on a smooth horizontal surface. Two other parallel conductor rest on them at right angles so as from B exits vertical. A uniform magnetic field B exists a vertical direction. Now all the four conductors stock moving outwards with a constant velocity v. The induced emf e and induced current i will vary wide time t as
A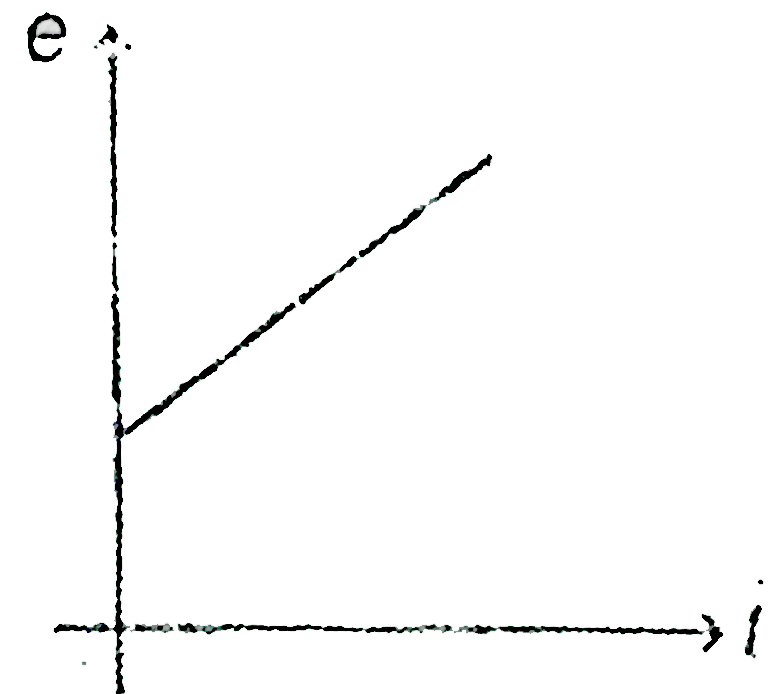

B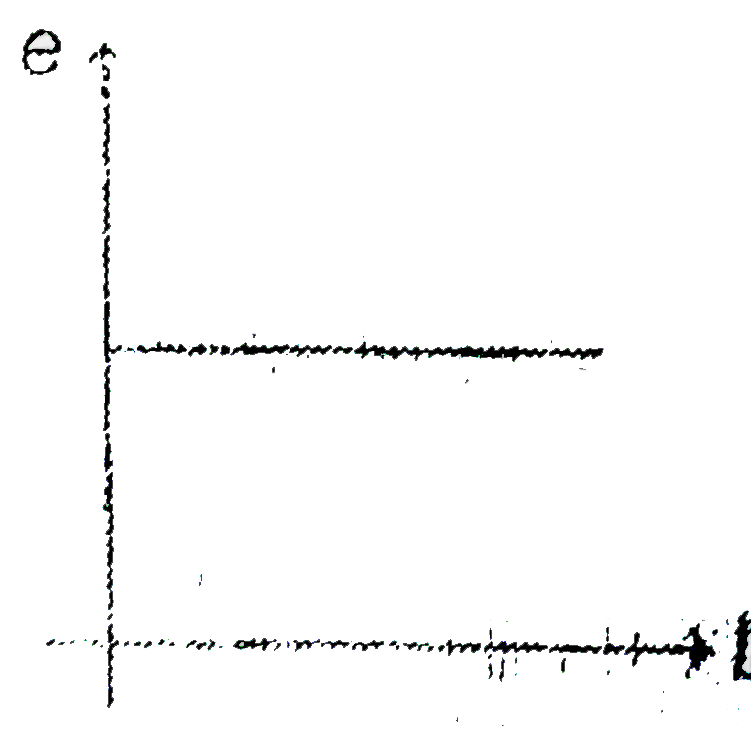

C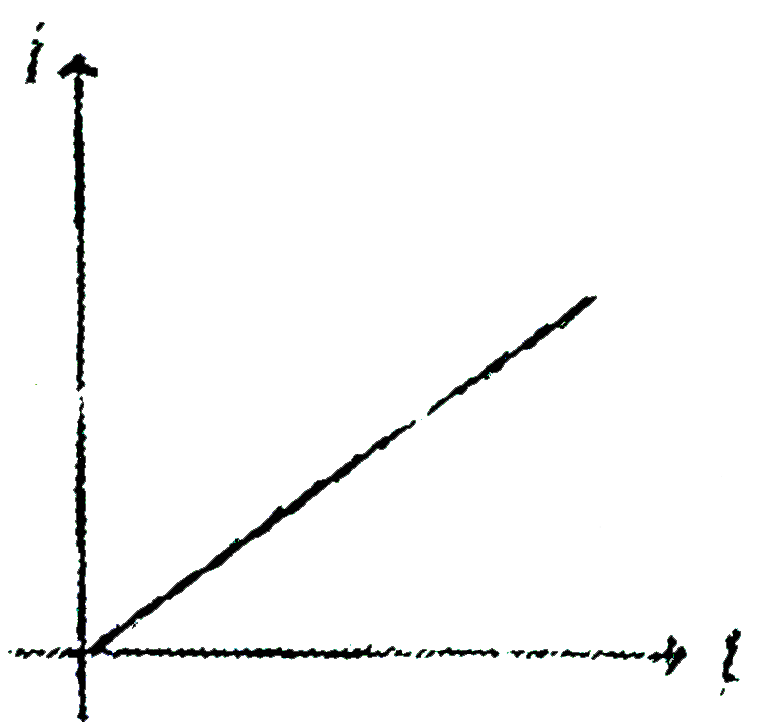

D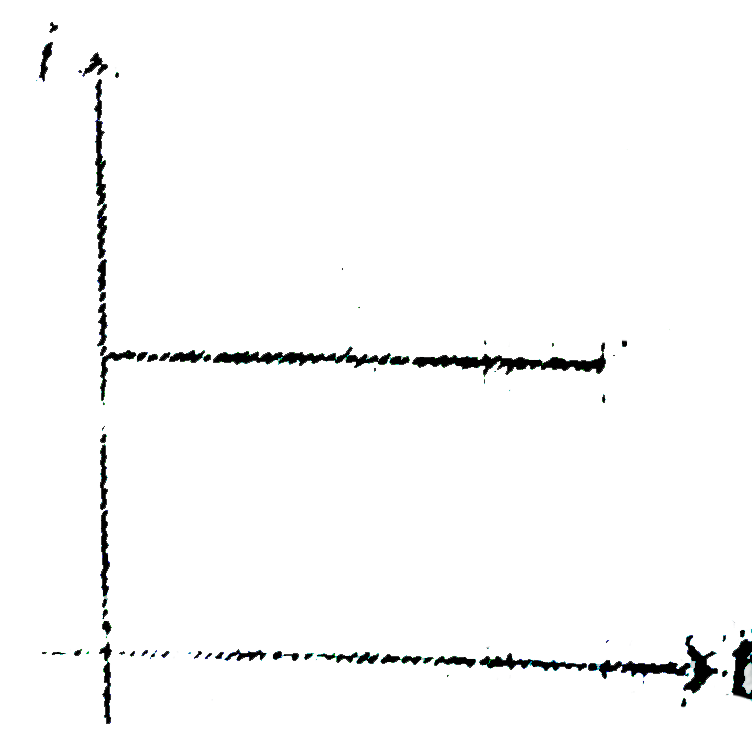
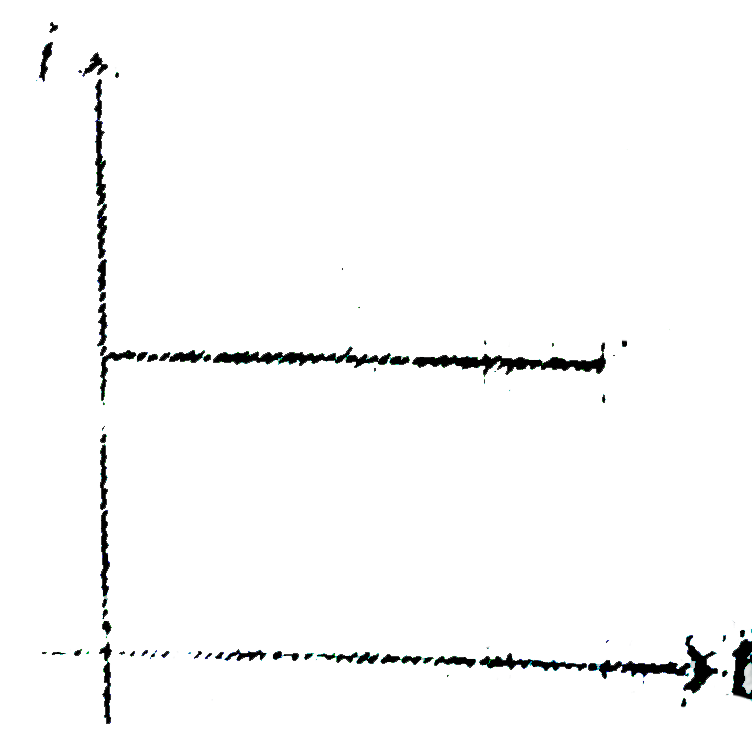
Text Solution
AI Generated Solution
The correct Answer is:
To solve the problem, we need to analyze the situation involving the four conductors, the magnetic field, and the motion of the conductors. Here’s a step-by-step breakdown of the solution:
### Step 1: Understand the Setup
We have two long straight conductors lying horizontally and two other conductors resting on them at right angles. A uniform magnetic field \( B \) is directed vertically, and all four conductors are moving outward with a constant velocity \( v \).
### Step 2: Determine the Change in Area
Initially, let the side length of the area formed by the conductors be \( a \). As the conductors move outward, the distance between them increases. After a time \( t \), each conductor moves a distance \( vt \). Therefore, the new side length \( a' \) becomes:
\[
a' = a + 2vt
\]
The area \( A \) at any time \( t \) is given by:
\[
A = (a + 2vt)^2
\]
### Step 3: Calculate the Rate of Change of Area
To find the induced EMF, we need to calculate the rate of change of area with respect to time:
\[
\frac{dA}{dt} = \frac{d}{dt}[(a + 2vt)^2] = 2(a + 2vt) \cdot \frac{d}{dt}(a + 2vt) = 2(a + 2vt) \cdot 2v = 4v(a + 2vt)
\]
### Step 4: Calculate the Rate of Change of Magnetic Flux
The magnetic flux \( \Phi \) through the area is given by:
\[
\Phi = B \cdot A
\]
Thus, the rate of change of magnetic flux is:
\[
\frac{d\Phi}{dt} = B \cdot \frac{dA}{dt} = B \cdot 4v(a + 2vt)
\]
### Step 5: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF \( e \) is equal to the negative rate of change of magnetic flux:
\[
e = -\frac{d\Phi}{dt} = -B \cdot 4v(a + 2vt)
\]
Since we are interested in the magnitude, we can ignore the negative sign:
\[
e = 4Bv(a + 2vt)
\]
### Step 6: Calculate the Induced Current
The resistance \( R \) of the conductors can be expressed in terms of their resistance per unit length \( r \) and the total length of the conductors. The total resistance \( R \) at any time is:
\[
R = r \cdot (4(a + 2vt))
\]
Thus, the induced current \( i \) can be calculated using Ohm's law \( i = \frac{e}{R} \):
\[
i = \frac{4Bv(a + 2vt)}{r \cdot (4(a + 2vt))} = \frac{Bv}{r}
\]
This shows that the induced current \( i \) is constant over time since it does not depend on \( t \).
### Conclusion
- The induced EMF \( e \) increases with time as \( e = 4Bv(a + 2vt) \).
- The induced current \( i \) remains constant as \( i = \frac{Bv}{r} \).
Similar Questions
Explore conceptually related problems
Two parallel long straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angle so as to form a square of side a. A uniform magnetic field B exists at right angle to the plane containing the conductors. Now, conductors starts moving outward witha constant velocity v_0 at t=0 . Then, induced current in the loop at any time is (lamda is resistance per unit length of the conductors)
Two parallel, long, straight conductor lie on a smooth plane surface. Two other parallel so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the cinductors. Now they start moving out with a constant velocity v . (A) Will the induced emf be time dependent? (b) Will the current be time dependent ?
Figure shows a wire sliding on two parallel, conducting rails placed at a separation L . A magnetic field B exists in a direction perpendicular to the plane of the rails. What force is necessary to keep the wire moving at a constant velocity V ?
A square loop of edge a having n turns Is rotated with a uniform angular velocity omega about one of its diagonals which is kept fixed in a horizontal position . A uniform magnetic field B exists in the vertical direction. Find the emf induced in the coil.
A conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
A conducting rod of length 2l is rotating with constant angular speed w about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The e.m.f. induced between two ends of the rod is
Two parallel fixed conducting rails are l distance apart. They are connected by a conducting wire xy. A uniform magnetic field B is applied normal to its plane. Two other rods PQ and RT(RS = ST) are moved with a constant velocity v. Resistance/ length of these two rods are lamda no other wire has resistance. Then :
A straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms^(-1) and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
A loop is formed by two parallel conductors connected by a selenoid with inductance L and a condutcing rod of mass which can freely (without friction) slide over the conductors. The conductors are located in a horizontal plane in as uniform vertical magnetic field B .The distance between the conductors is l . At the moment t=0 the rod is impart the initial velocity v_0 directed to the right. find the equation of its motion d(t) if the electric resistance of the loop is negligible
A square loop of edge b having M turns is rotated with a uniform angular velocity omega about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B_(0) exists in the vertical direction. Find (i) the emf induced in the coil as a function of time t. (ii) the maximum emf induced. (iii) the average emf induced in the loop over a long period. (iv) if resistance of loop is R, amount of charge flown in time t = 0 to t = 2T. (v) heat produced in time t = 0 to t = 2T.
Recommended Questions
- Two parallel long straight conductors lie on a smooth horizontal surfa...
Text Solution
|
- Two parallel long straight conductors lie on a smooth plane surface. T...
Text Solution
|
- Two parallel, long, straight conductor lie on a smooth plane surface. ...
Text Solution
|
- Two parallel long straight conductors lie on a smooth surface. Two oth...
Text Solution
|
- A conductor PQ , with PQ=r , moves with a velocity v in a uniform magn...
Text Solution
|
- Two parallel long straight conductors lie on a smooth horizontal surfa...
Text Solution
|
- A straight conductor 0.1 m long moves in a uniform magnetic field 0.1 ...
Text Solution
|
- Two straight long parallel conductors are moved towards each other. A ...
Text Solution
|
- A conductor is moving with the velocity v in the magnetic field and in...
Text Solution
|