Home
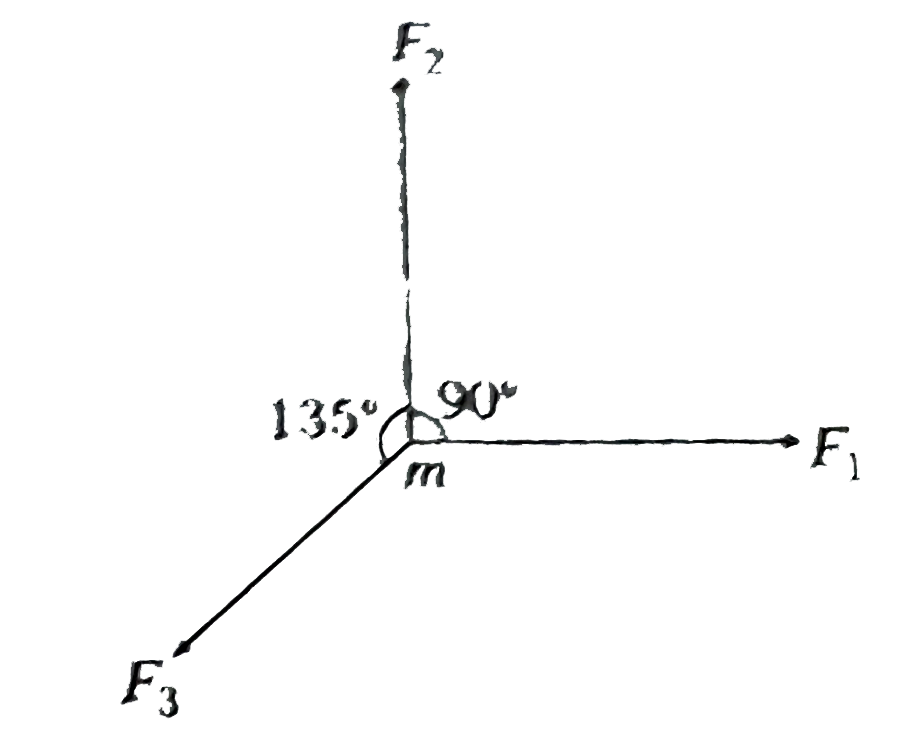
Class 11
PHYSICS
When a force F acts on a body of mass m ...

When a force F acts on a body of mass m the acceleration product in the body is a . If three equal forces `F_(1)=F_(2)=F_(3)=F` act on the same body as shown in figure the acceleration produced is

A

`(sqrt(2)-1)a`

B

`(sqrt(2)+1)a`

C

`sqrt(2)a`

D

a

Text Solution

Verified by Experts

The correct Answer is:
A
(a) Accelertion `a=(F)/(m)`
Resultant of `F_(1)andF_(2)`will be
`F_(12)=sqrt(2F)`(in opposite directiomn o f`F_(3)`)
Now ,resultant of`F_(12)and F_(3)`will be ,
`F_("net")=(sqrt(2)-1)F`
`thereforea=(F_("net"))/(m)=(sqrt(2)-1)(F)/(m)=(sqrt(2)-1)a`
Promotional Banner

Topper's Solved these Questions

  • BASIC MATHEMATICS

    DC PANDEY ENGLISH|Exercise Exercise|13 Videos

  • CALORIMETRY & HEAT TRANSFER

    DC PANDEY ENGLISH|Exercise Level 2 Subjective|14 Videos

Similar Questions

Explore conceptually related problems

When a force F acs on a body of mass m the acceleration product in the body is a . If htree equal forces F_(1)=F_(2)=F_(3)=F act on the same body as shown in figure the accleration produced is

A force of 10 N acts on a body of mass 5 kg. Find the acceleration produced.

A force of 15 N acts on a body of mass 2 kg. Calculate the acceleration produced.

A force of 15 N acts on a body of mass 2 kg. Calculate the acceleration produced.

Two forces F_(1) " and " F_(2) are acting on a rod abc as shown in figure.

When a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is

According to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F_(1) and F_(2) are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F_(1) (in newton)

Four forces are acting on a body as shown in figure. The magnitude of resultant of the forces is

A force produces an acceleration of a_(1) in a body and the same force produces an acceleration of a_(2) in another body. If the two bodies are combined and the same force is applied on the combination, the acceleration produced in it is

A force produces an acceleration of 4ms^(-2) in a body of mass m_(1) and the same force produces an acceleration of 6ms^(-2) in another body oa mass m_(2) . If the same force is applied to (m_(1)+m_(2)) , then the acceleration will be