A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
DC PANDEY ENGLISH|Exercise (B) Meical entrance special format questions (Assertion and reason)|19 VideosMOTION IN A PLANE
DC PANDEY ENGLISH|Exercise (B) Meical entrance special format questions (Mathch the columns)|6 VideosMOTION IN A PLANE
DC PANDEY ENGLISH|Exercise Check point 3.7|15 VideosMOTION
DC PANDEY ENGLISH|Exercise Medical entrances gallery|19 VideosPROJECTILE MOTION
DC PANDEY ENGLISH|Exercise Level - 2 Subjective|10 Videos
Similar Questions
Explore conceptually related problems
DC PANDEY ENGLISH-MOTION IN A PLANE-(A) Taking it together
- A cyclist starts from the centre O of a circular park of radius 1 km. ...
Text Solution
|
- A particle moves along a straight line OX. At a time t(in second), the...
Text Solution
|
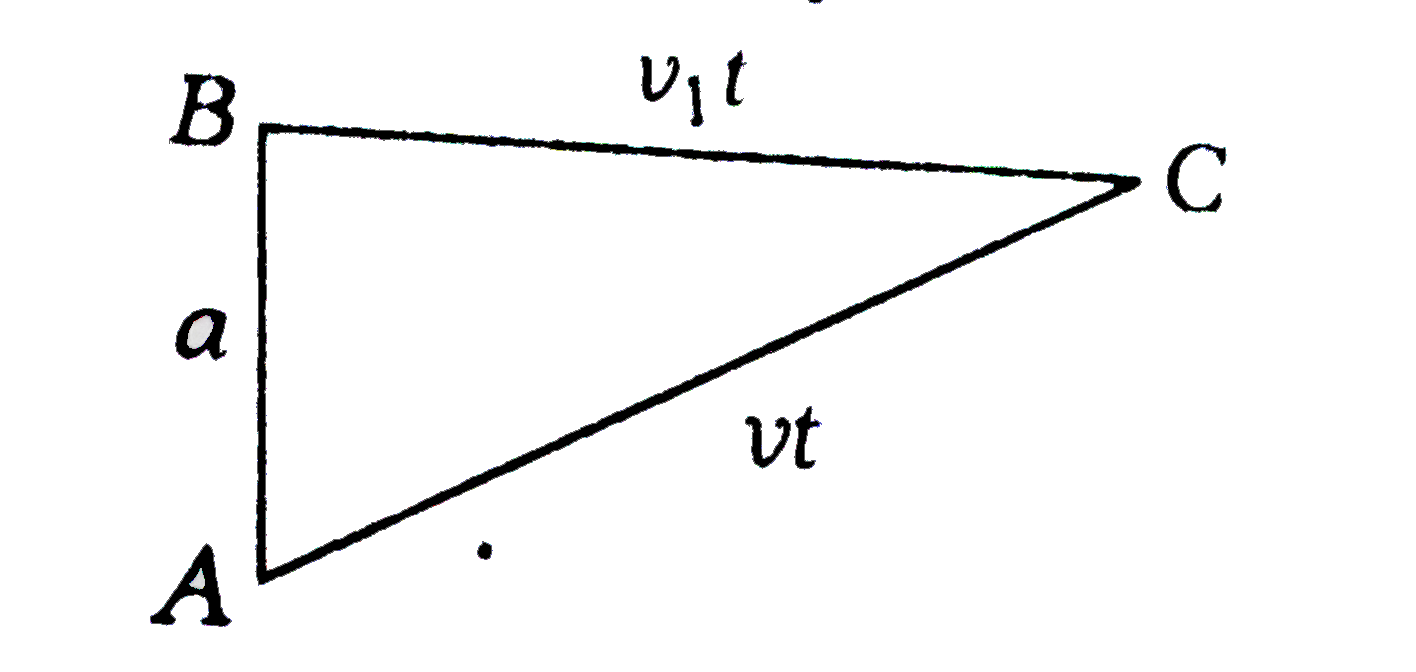
- Two boys are standing at the ends A and B of a ground where AB = a. Th...
Text Solution
|
- A bullet emerges from a barrel of length 1.2 m with a speed of 640 ms^...
Text Solution
|
- From the top of a tower, 80m high from the ground a stone is thrown in...
Text Solution
|
- A boggy of uniformly moving train is suddenly detached from train and ...
Text Solution
|
- A man is 45 m behind the bus when the bus starts acceleration from res...
Text Solution
|
- A body moves for a total of nine second starting from rest with unifor...
Text Solution
|
- A point initially at rest moves along x-axis. Its acceleration varies ...
Text Solution
|
- The time taken by a block of wood (initially at rest) to slide down a ...
Text Solution
|
- A particle move a distance x in time t according to equation x = (t + ...
Text Solution
|
- A ball is thrown upwards with a speed u from a height h above the grou...
Text Solution
|
- The position of a particle along X-axis at time t is given by x=2+t-3t...
Text Solution
|
- A ball falls freely from rest. The ratio of the distance travelled in ...
Text Solution
|
- What is nature of trajectory of a particle having a uniformly accelera...
Text Solution
|
- A particle moves along a straight line. Its position at any instant is...
Text Solution
|
- A point moves in a straight line so its displacement x meter at time t...
Text Solution
|
- The displacement x of a particle varies with time t as x = ae^(-alpha ...
Text Solution
|
- Galileo's law of odd number: The distances traversed, during equal int...
Text Solution
|
- A particle starting from rest. Its acceleration (a) versus time (t) is...
Text Solution
|