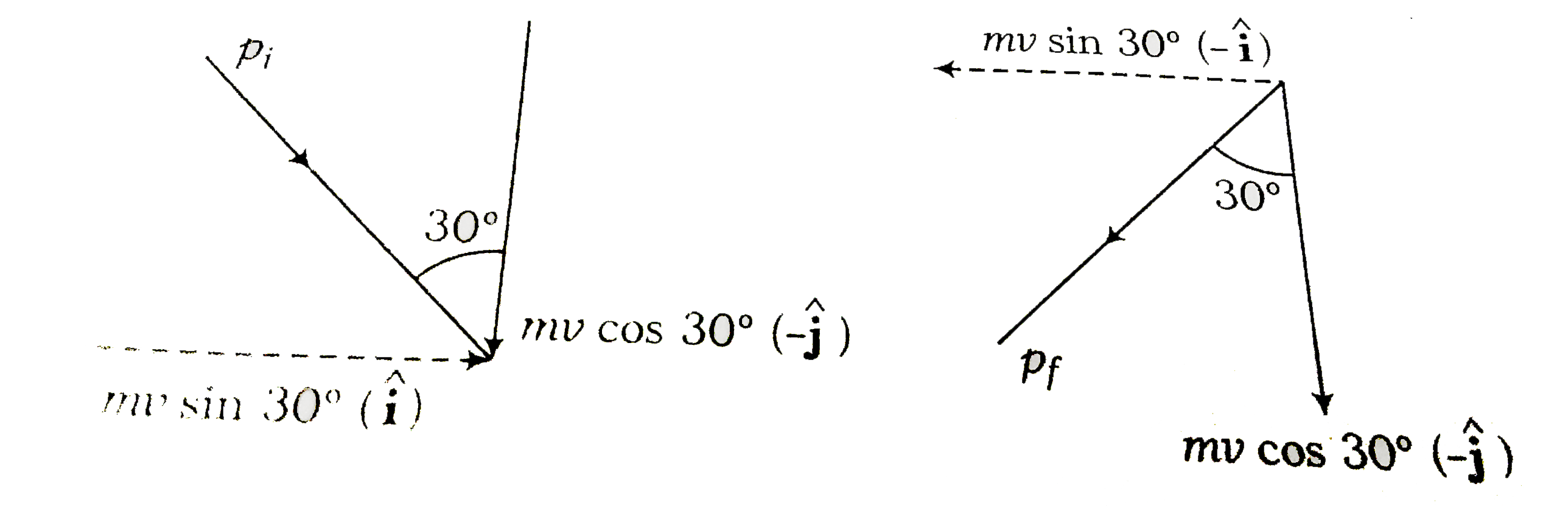Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- A riding ball of mass m strikes a rigid wall at 60^(@) and gets reflec...
Text Solution
|
- A riding ball of mass m strikes a rigid wall at 60^(@) and gets reflec...
Text Solution
|
- A ball of mass m strikes a rigid walJ with speed u and rebounds with t...
Text Solution
|
- A ball of mass m strikes a rigid walJ with speed u and rebounds with t...
Text Solution
|
- A rigid ball of mass m strikes a rigid wall at 60^(@) and gets reflect...
Text Solution
|
- m द्रव्यमान की एक दृढ़ गेंद किसी दृढ़ दीवार से 60^(@)पर टकराकर प्रवर्तित...
Text Solution
|
- A ball of mass m strikes a rigid wall with speed v and gets reflected ...
Text Solution
|
- m द्रव्यमान की एक सख्त गेंद (बॉल) किसी दृढ़ दीवार से नीचे आरेख में दर्...
Text Solution
|
- A rigid ball of mass m strikes a rigid wall at 60° and gets reflected ...
Text Solution
|