Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
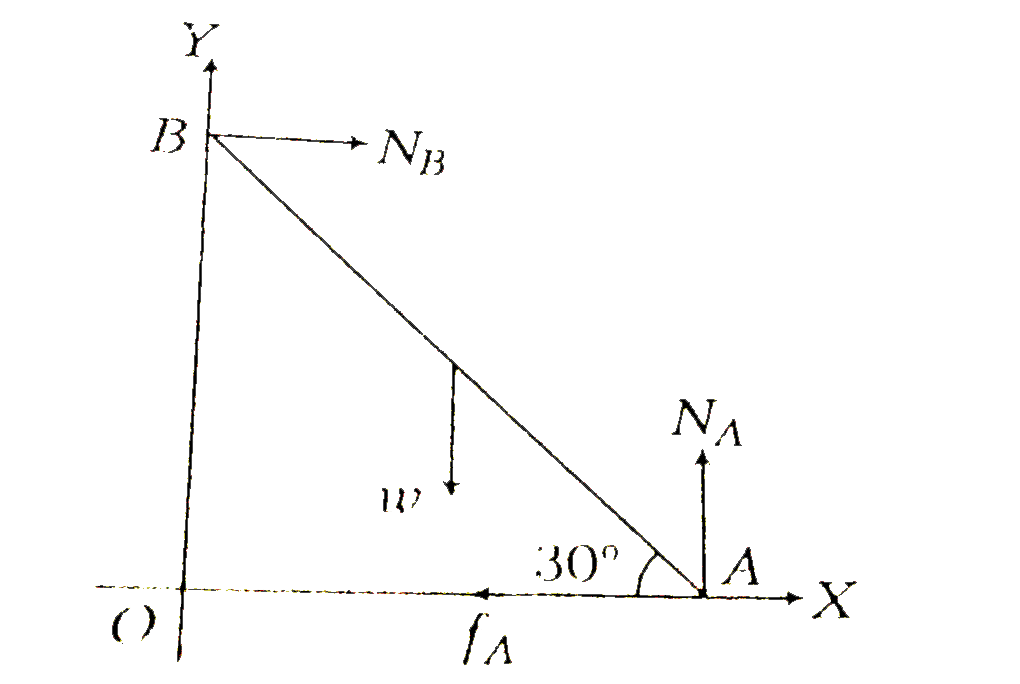
- A rod AB rests with the end A on rough horizontal ground and the end B...
Text Solution
|
- A uniform rod of length L rests against a smooth roller as shown in fi...
Text Solution
|
- A rod of weight w is supported by two parallel knife edges A and B and...
Text Solution
|
- A rod AB rests with the end A on rough horizontal ground and the end B...
Text Solution
|
- A uniform rod of length L rests against a smooth roller as shown in fi...
Text Solution
|
- A uniform rod of mass m and length L is held at rest by a force F appl...
Text Solution
|
- A rod AB of mass M and length L is shown in figure. End A of rod is hi...
Text Solution
|
- एक छड़ का भार W है। यदि दो समांतर क्षुरधारों A तथा B पर टिकी है तथा क्ष...
Text Solution
|
- A uniform solid rod of mass 40kg and length 10m rests against a vertic...
Text Solution
|