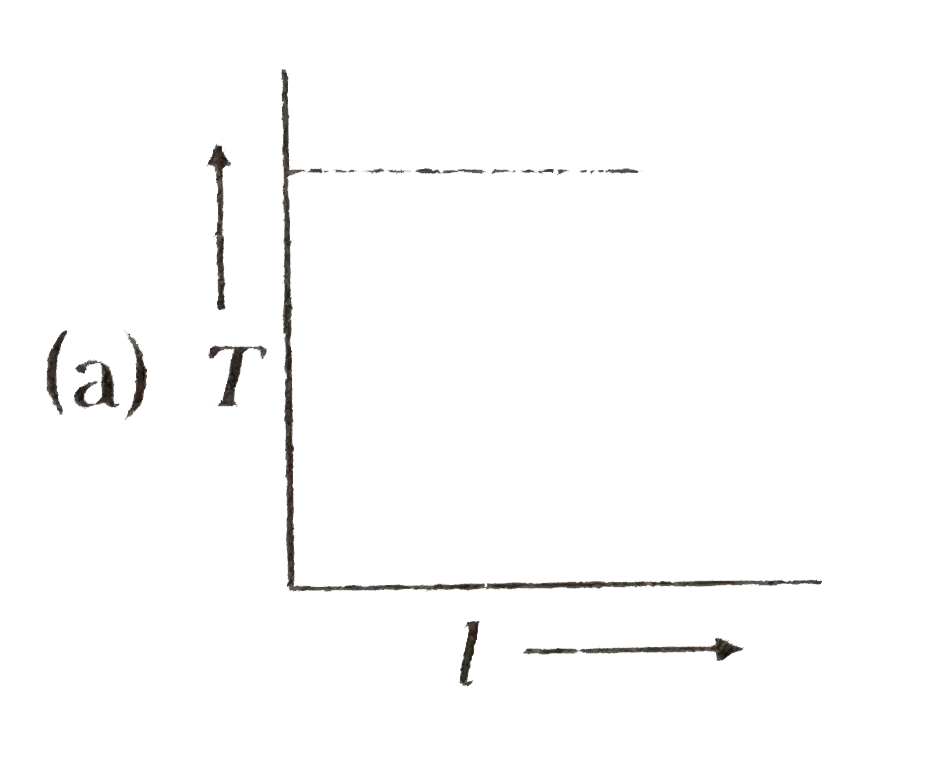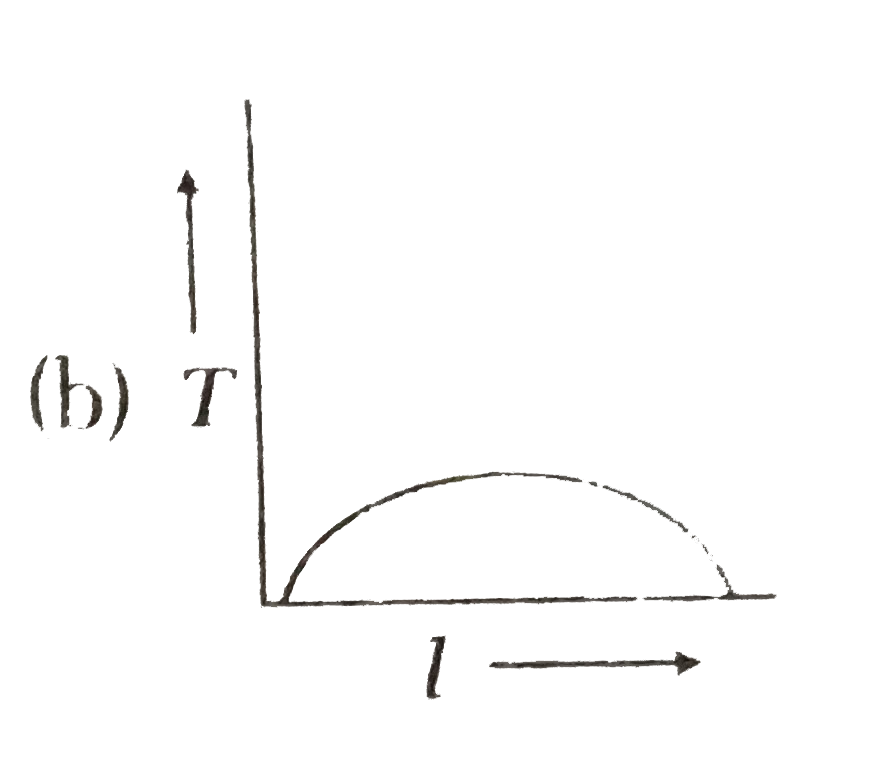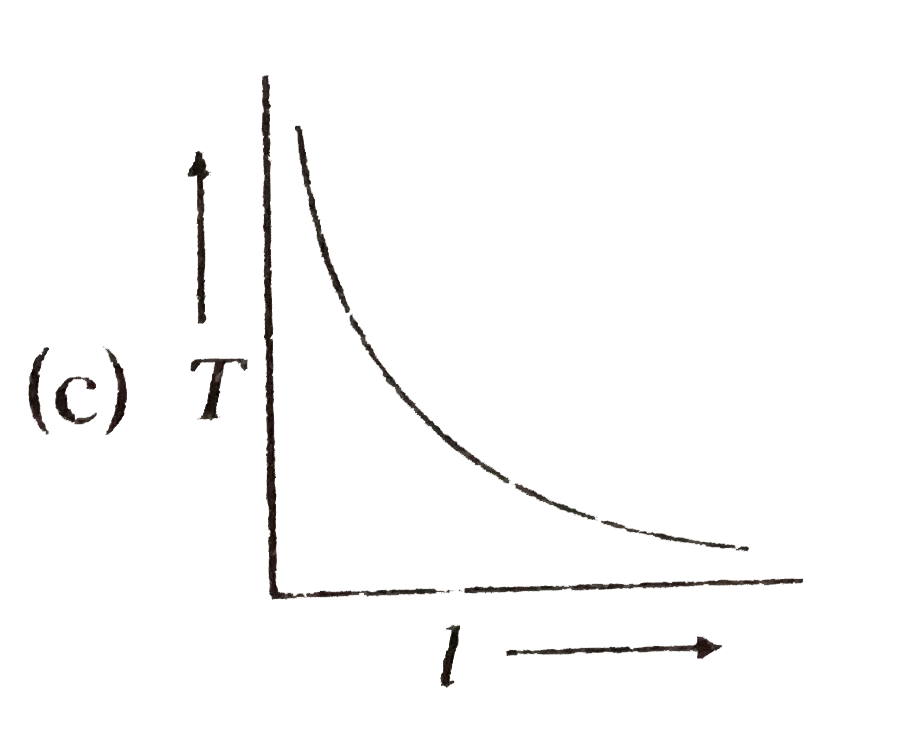A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In case of a simple pendulum, time period versus length is depicted by
Text Solution
|
- In case of a simple pendulum, time period versus length is depicted by
Text Solution
|
- Simple pendulum is executing simple harmonic motion with time period T...
Text Solution
|
- For a simple pendulum the graph between length and time period will be
Text Solution
|
- The time period of a simple pendulum of infinte length is
Text Solution
|
- The time period of a simple pendulum of length 9.8 m is
Text Solution
|
- A simple pendulum of length 25 cm has a time period of 1 s and another...
Text Solution
|
- If the length of a simple pendulum is increased by 2%, then the time p...
Text Solution
|
- The graph between the time period and the length of a simple pendulum ...
Text Solution
|