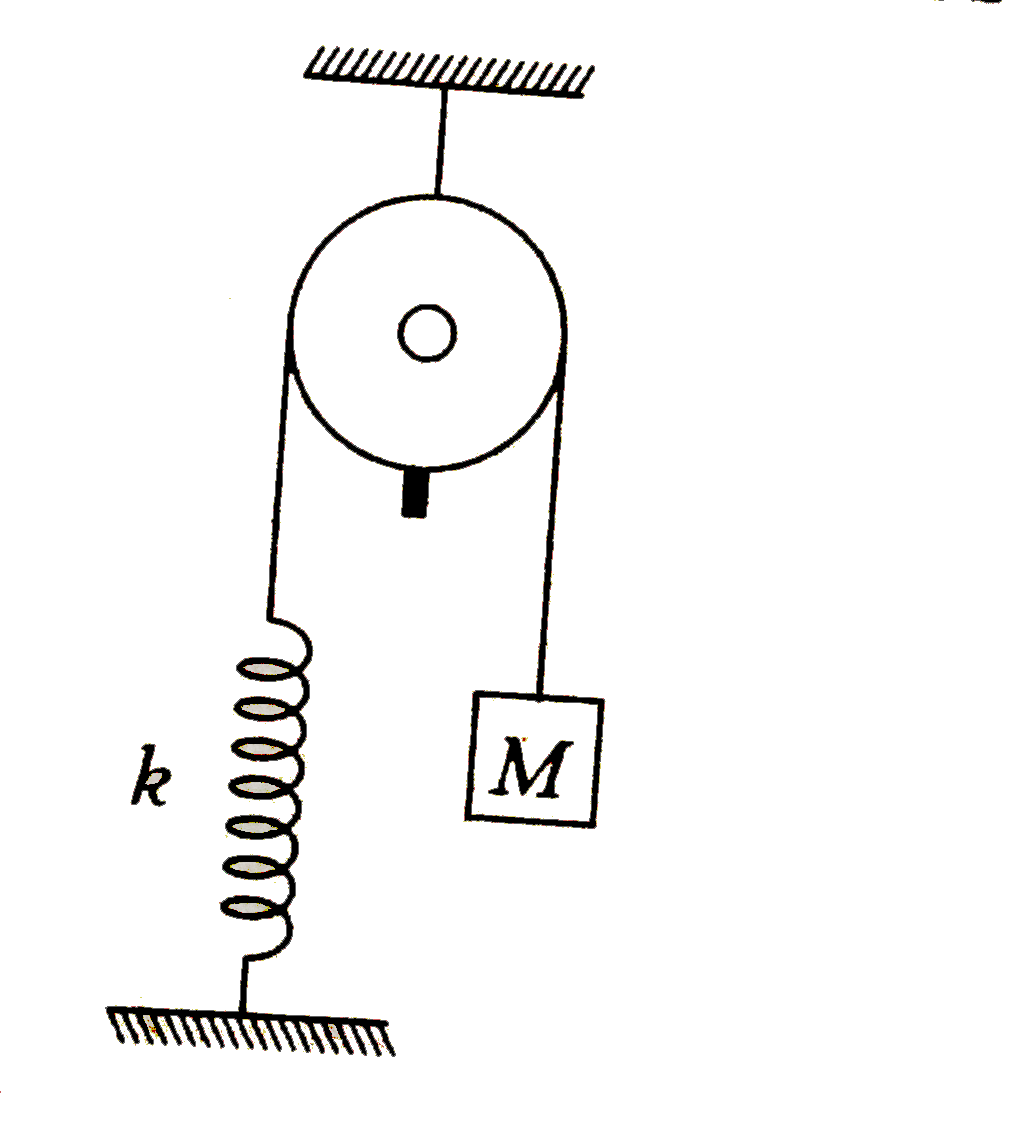A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A mass M=5 kg is attached to a string as shown in the figure and held ...
Text Solution
|
- A mass m = 8 kg is attached to a spring passing over a pulled whose ot...
Text Solution
|
- A load of mass M is attached to the bottom of a spring of mass 'M //3'...
Text Solution
|
- When a mass M is attached to the spring of force constant k , then the...
Text Solution
|
- A mass m = 8kg is attached to a spring as shown in figure and held in ...
Text Solution
|
- A mass M=5 kg is attached to a string as shown in the figure and held ...
Text Solution
|
- दो पिण्ड P ( द्रव्यमान 2 किग्रा) तथा Q ( द्रव्यमान 1 किग्रा) एक स्प्र...
Text Solution
|
- A block of mass m is attached to a cart of mass 4m through spring of s...
Text Solution
|
- Two springs of spring constant k(1)and k(2) are connected by a mass m ...
Text Solution
|