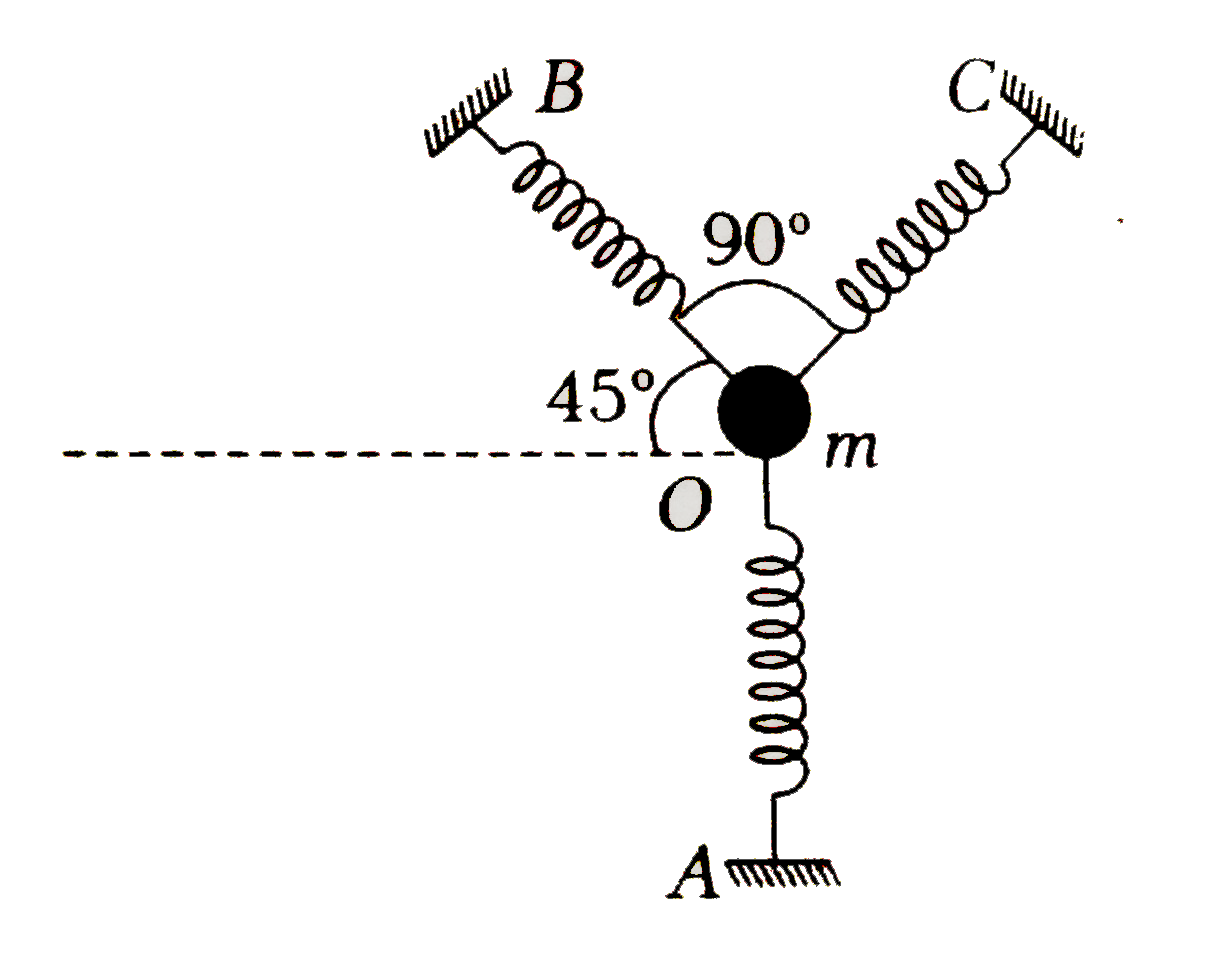A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A mass M is attached to a horizontal spring of force constant k fixed ...
Text Solution
|
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- When a mass M is attached to the spring of force constant k , then the...
Text Solution
|
- Tow identical springs of spring constant k are attached to a block of ...
Text Solution
|
- A mass M is attached to a horizontal spring of force constant k fixed ...
Text Solution
|
- Block A of mass m is performing SHM of amplitude a. Another block B of...
Text Solution
|
- Two identical springs of spring constant k are attached to a block of ...
Text Solution
|
- The period of oscillation of a mass M, hanging from a spring of force ...
Text Solution
|
- A mass m is attached to the free end of a massless spring of spring co...
Text Solution
|