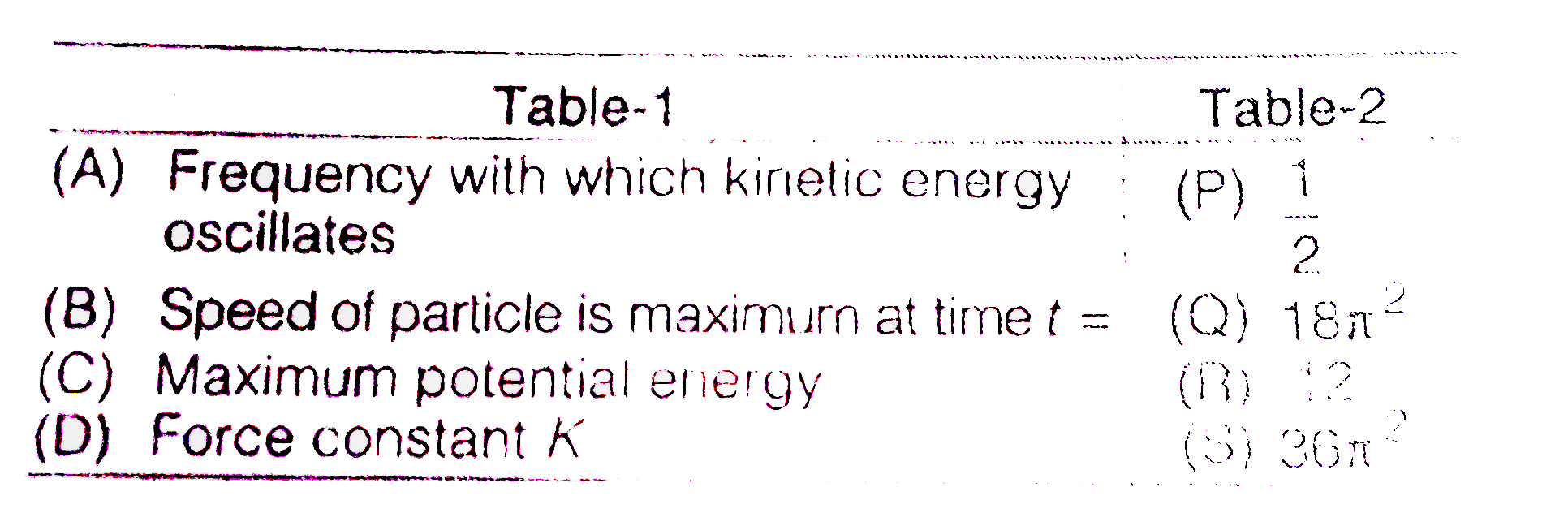Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- x-t equation of a particle in SHM is given as x=1.0sin(12pit) in SI un...
Text Solution
|
- Displacement-time equation of a particle moving along x-axis is x=20+t...
Text Solution
|
- A 2.0 kg particle undergoes SHM according to x = 15 sin ((pi t)/(4) + ...
Text Solution
|
- If the displacement relation for a particle in a wave is given by y=5 ...
Text Solution
|
- x-t equation of a particle in SHM is given as x=1.0sin(12pit) in SI un...
Text Solution
|
- Assertion : x-t equation of a particle in SHM is given as : x=A "cos"o...
Text Solution
|
- A particle executing SHM according to the equation x=5cos(2pit+(pi)/(4...
Text Solution
|
- A particle of mass 1 kg executing S.H.M. is given by y = 2 cos (10t+pi...
Text Solution
|
- A particle executing SHM according to the equation x=5cos(2pit+(pi)/(4...
Text Solution
|