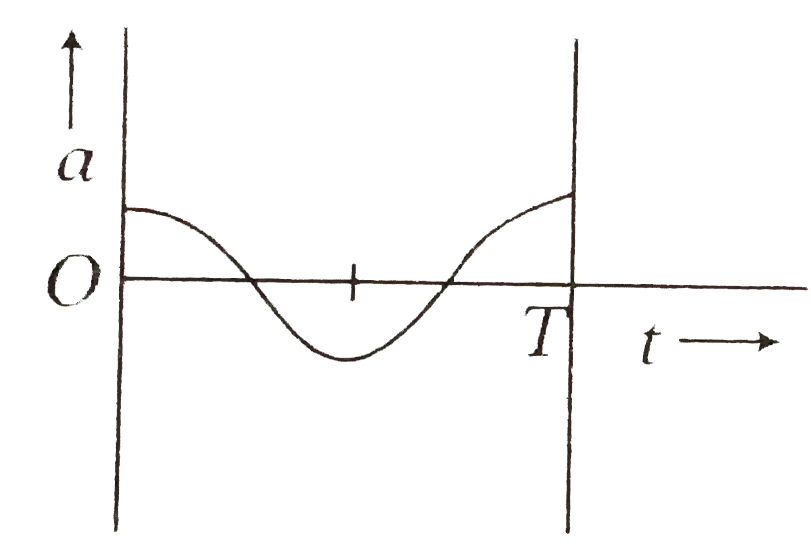
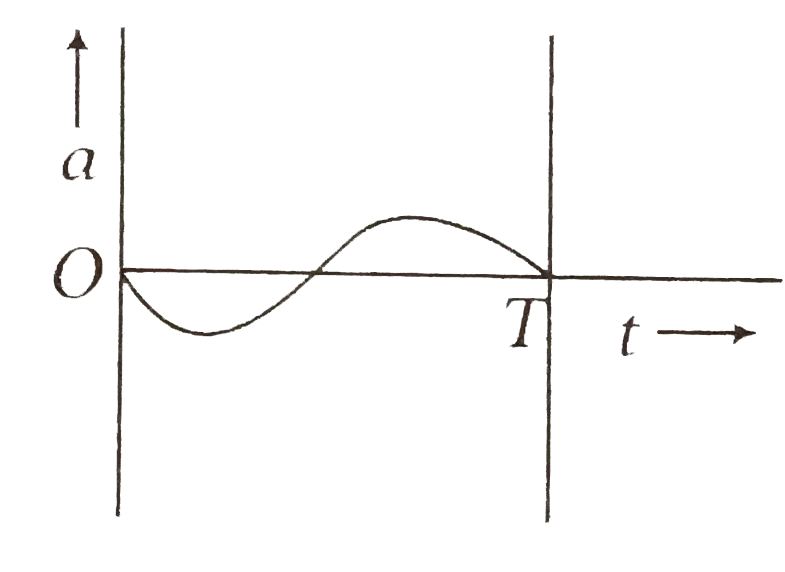
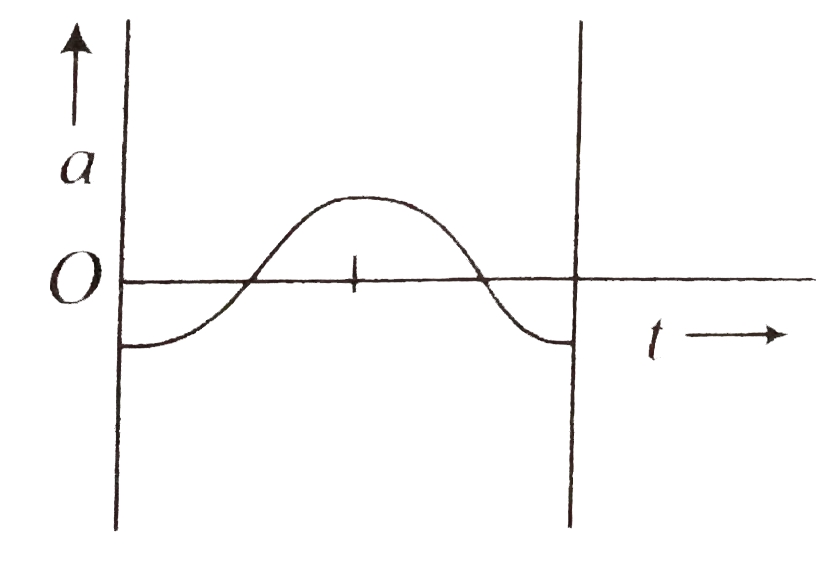
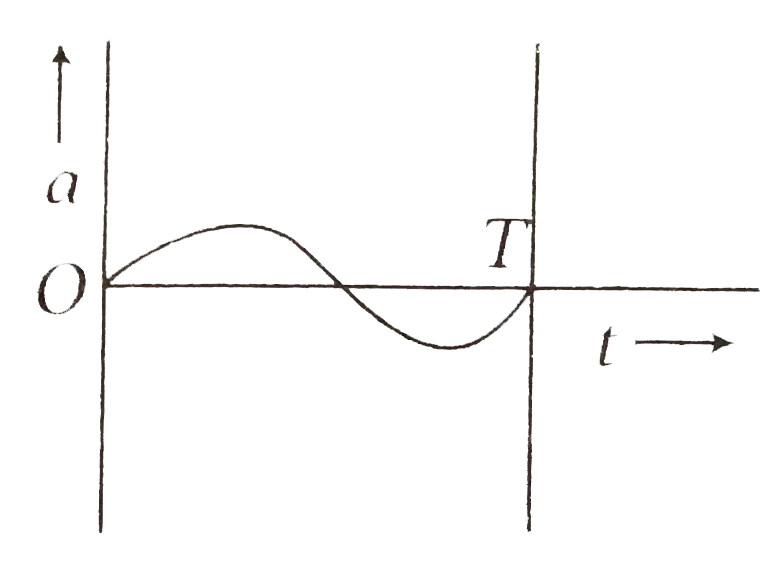
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The oscillation of a body on a smooth horizental surface is respresent...
Text Solution
|
- The oscillation of a body on a smooth horizental surface is respresent...
Text Solution
|
- The oscillationof a body on a smooth horizontal surface is represented...
Text Solution
|
- The oscillation of a body on a smooth horizontal surface is represente...
Text Solution
|
- The oscillation of a body on a smooth horizontal surface is represente...
Text Solution
|
- एक चिकने क्षैतिज तल पर किसी पिण्ड के दोलन निम्न सूत्र द्वारा प्रदर्शित...
Text Solution
|
- The oscillation of a body on a smooth horizontal surface is represente...
Text Solution
|
- The oscillation of a body on a smooth horizontal surface is represente...
Text Solution
|
- The oscillation of a body on a smooth horizontal surface is represente...
Text Solution
|