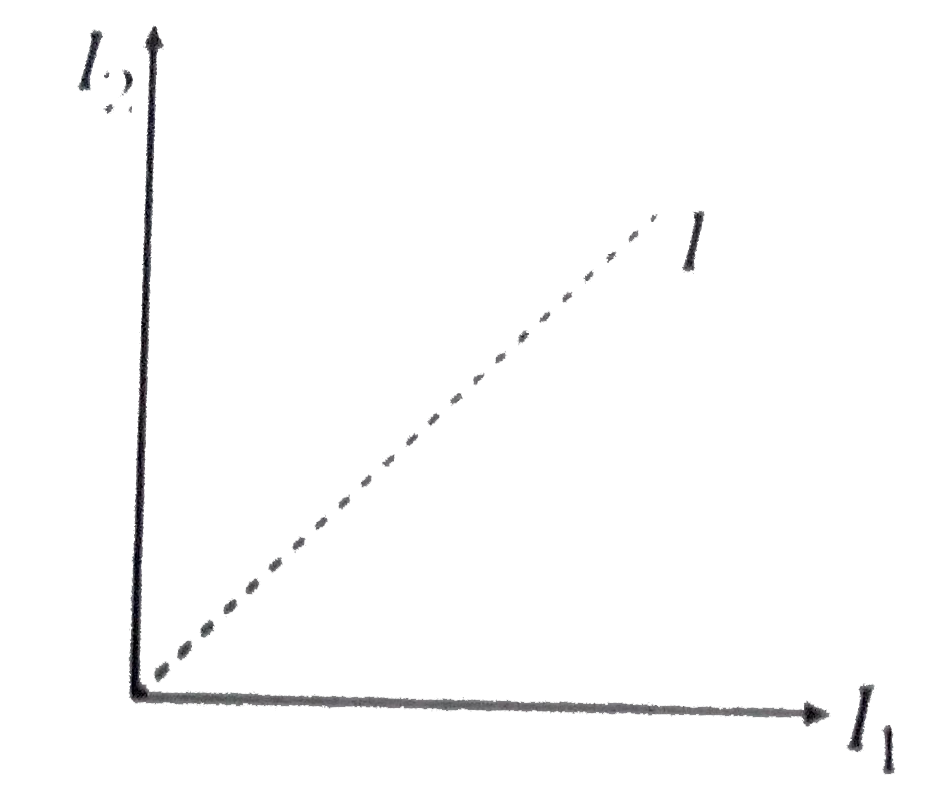
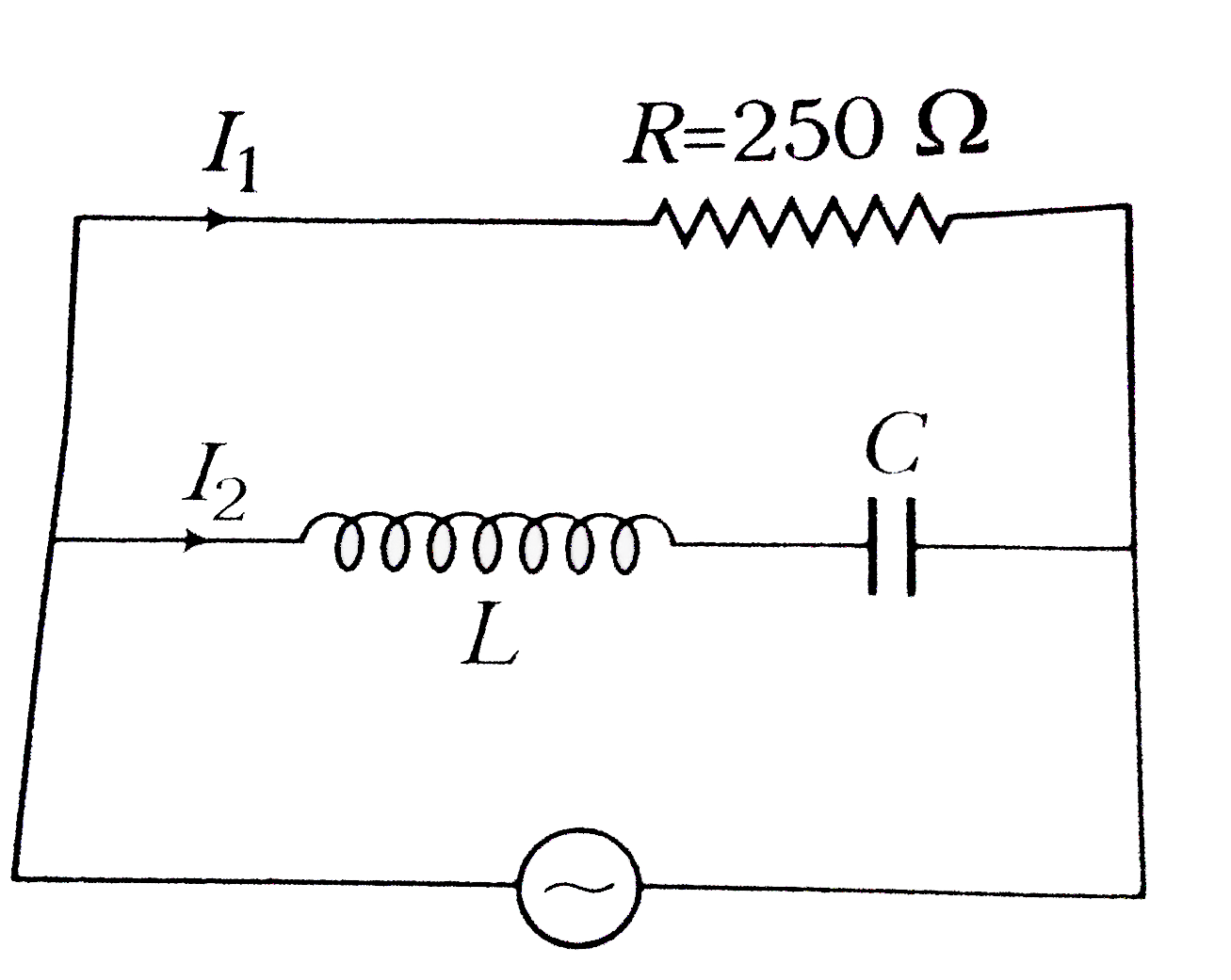Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Inductance (L), capacitance (C) and resistance (R) are constained in a...
Text Solution
|
- A current of 4 A flows in a coil when connected to a 12 V dc source. I...
Text Solution
|
- A box contains L,C and R When 250V dc is applied to the terminals of t...
Text Solution
|
- Inductance (L), capacitance (C) and resistance (R) are constained in a...
Text Solution
|
- A current of 6 A flows in a coil when connected to a dc source of 18 V...
Text Solution
|
- 60 muF धारिता का संधारित्र (capacitor) 110 V, 60 Hz के प्रत्यावर्ती ...
Text Solution
|
- Resistor of resistance R and capacitor of capacitance C are connected ...
Text Solution
|
- There is an AC source of rms voltage 200 V and frequency 50 Hz. When t...
Text Solution
|
- एक शुद्ध प्रेरणिक ac परिपथ में L = 25.0 mH और rms वोल्टता, 150 V है। प...
Text Solution
|