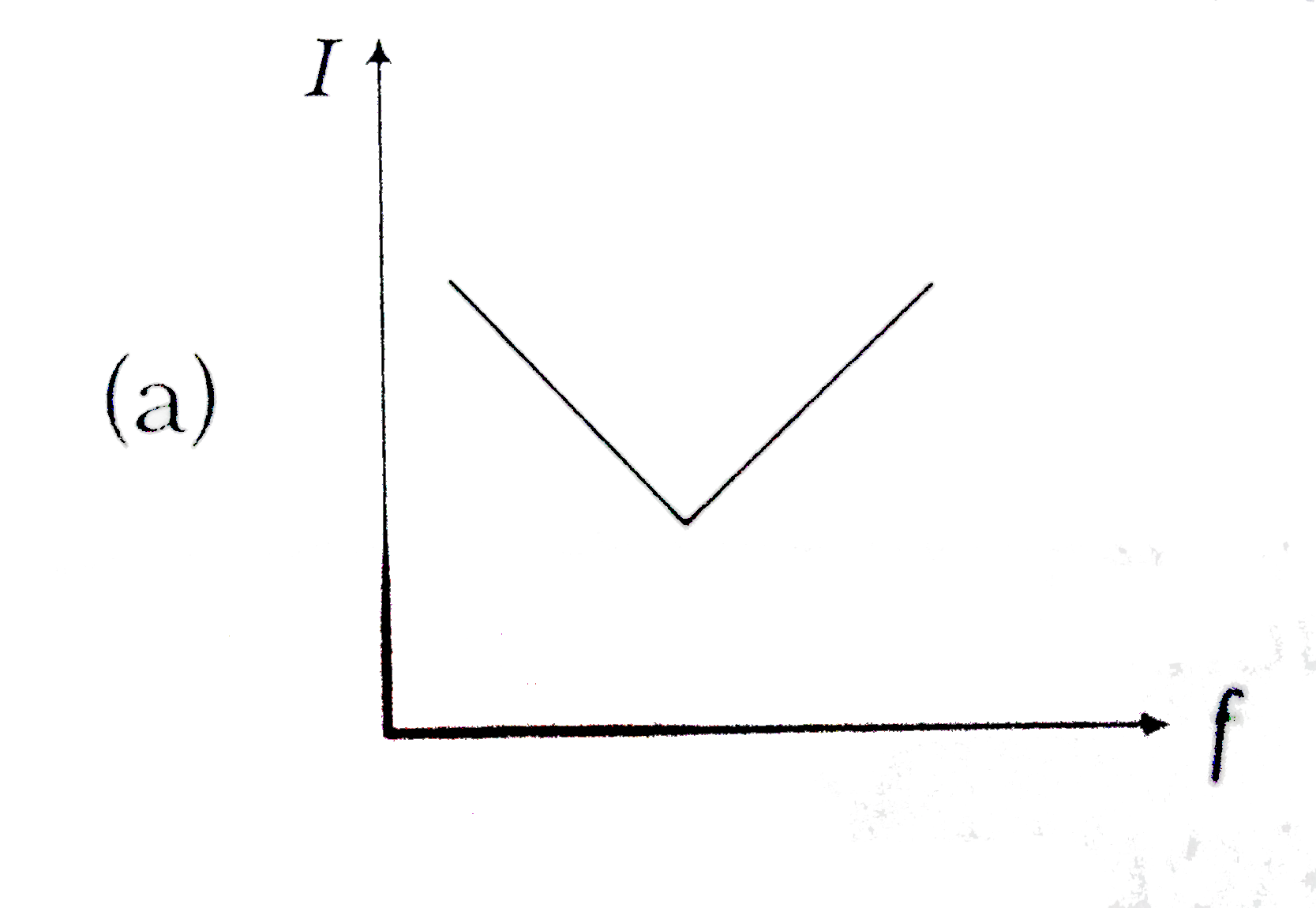
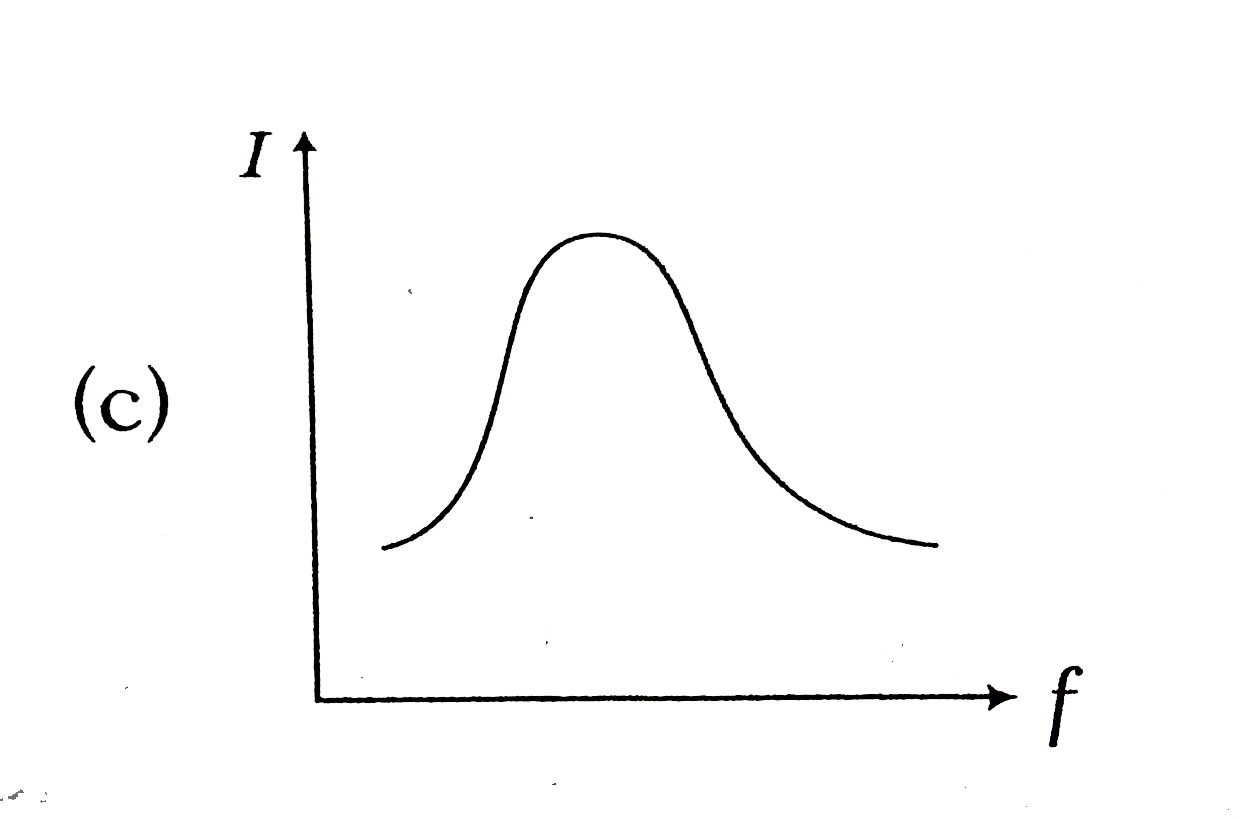
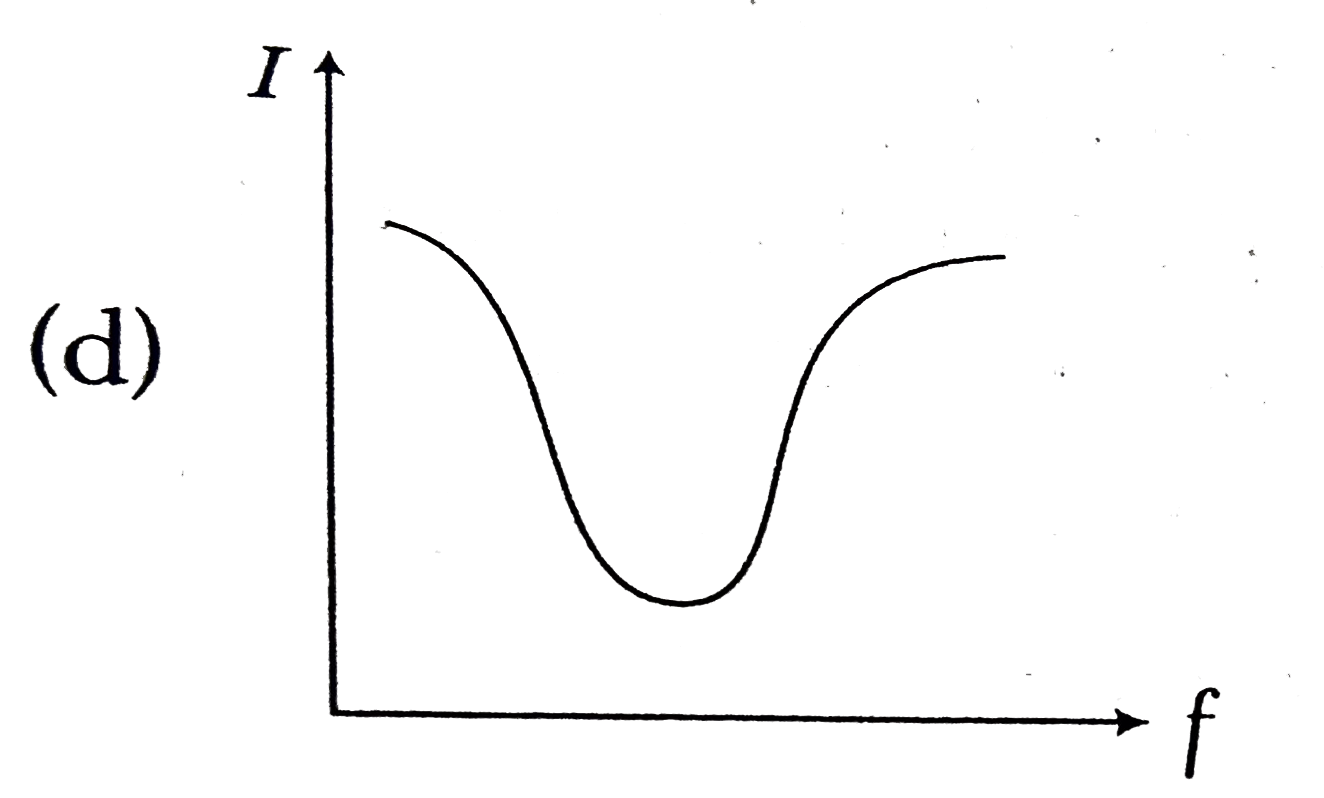
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An AC source of variable frequency f is connected to an LCR series cir...
Text Solution
|
- An AC source of variable frequency f is connected to an LCR series cir...
Text Solution
|
- Figure shows a series LCR circuit connected to a variable frequency 23...
Text Solution
|
- Figure shows a series LCR circuit connected to a variable frequency 23...
Text Solution
|
- Figure shows a series LCR circuit connected to a variable frequency 23...
Text Solution
|
- In an LCR series ac circuit, the current is
Text Solution
|
- In LCR series AC circuit, the current
Text Solution
|
- Sketch graphs to show the variation of (i) current and (ii) impedance ...
Text Solution
|
- चित्र में एक श्रेणी LCR परिपथ प्रदर्शित किया गया है जिसमें L=5.0H,C = ...
Text Solution
|