Home
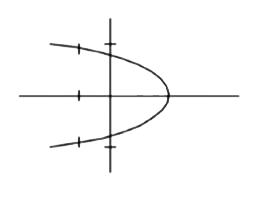
Class 11
MATHS
The curve is given by x = cos 2t, y = si...

The curve is given by `x = cos 2t, y = sin t` represents

A

A parabola

B

Circle

C

Part of a parabola

D

A pair of straight lines

Text Solution

Verified by Experts

The correct Answer is:
C

Given parabola equations are
`x=cos2t, y = sin t`
`rArr` Obviously, `x,y in [-1,1]`
`:.x=1-2sin^(2)t= 1-2y^(2)`
`rArr 2y^(2) =1-x= -(x-1)`
`rArr y^(2)= -(1)/(2) (x-1)`
`rArr` It represents a part of a parabola
Promotional Banner

Similar Questions

Explore conceptually related problems

x=a cos t, y=b sin t

x=2 cos^2 t, y= 6 sin ^2 t

If the parametric of a curve given by x=e^(t)cos t, y=et sin t , then the tangent to the curve at the point t=pi//4 makes with axis of x the angle

x = "sin" t, y = "cos" 2t

If a curve is given by x=a cos t+(b)/(2)cos2t and y=a sin t+(b)/(2)sin2t, then the points for which (d^(2)y)/(dx^(2))=0, are given by

The curve represented by x = 3 (cos t + sin t), y = 4 (cos t- sin t) is an ellipse whose eccentricity is e, such that 16e^2 + 7 is equal to:

The distance, from the origin, of the normal to the curve, x = 2 cos t + 2t sin t, y = 2 sin t - 2t "cos t at t" = (pi)/(4) , is :

If OT is the perpendicular drawn from the origin to the tangent at any point t to the curve x = a cos^(3) t, y = a sin^(3) t , then OT is equal to :

The curve represented by x=2(cos t+sin t) and y=5(cos t-sin t) is

Find the equation of tangent to the curve given by x=2 sin^(3)t ,y=2 cos^(3)t at a point where t=(pi)/(2) ?