Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
OSWAAL PUBLICATION-SOLVED PAPER II PUC APRIL-2016 -PART-D
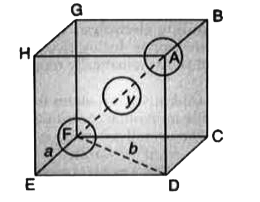
- a. Calculate the packing efficiency in a Body Centered Cubic (BCC) lat...
Text Solution
|
- a. Calculate the packing efficiency in a Body Centered Cubic (BCC) lat...
Text Solution
|
- 5.8 g of non - volatile, non - electrolyte solute was dissolved in 100...
Text Solution
|
- Mention any two differences between ideal and non-ideal solutions.
Text Solution
|
- State Faraday's First law of electrolysis. Write its mathematical form...
Text Solution
|
- State Kohlrausch law.
Text Solution
|
- Write the overall cell reaction taking place in Daniel Cell
Text Solution
|
- Derive an integrated rate equation for the rate constant of a zero ord...
Text Solution
|
- Draw a graph of potential energy v/s reaction co-ordinate showing the ...
Text Solution
|
- Mention any three differences between lyophilic and lyophobic colloids...
Text Solution
|
- What is heterogeneous catalysis ? Give an example.
Text Solution
|
- Explain the mechanism of SN1 reaction taking 2-bromo-2-methyl propane ...
Text Solution
|
- Explain wurtz-Fitting's reaction
Text Solution
|
- Write the general formula of Grignard reagent
Text Solution
|
- How is phenol manufactured by Cumene process?
Text Solution
|
- Among alcohols and phenols which one is more acidic?
Text Solution
|
- Explain the mechanism of addition of HCN to a carbonyl group in presen...
Text Solution
|
- How is bezamide obtained from benzoic acid ?
Text Solution
|
- Explain Carbyl amine reaction
Text Solution
|
- What is the action of bromine water on Benzenamine (Aniline) at room t...
Text Solution
|