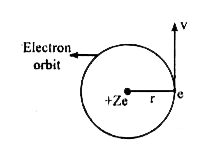
Text Solution
Verified by Experts
Topper's Solved these Questions
SUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
SUNSTAR PUBLICATION|Exercise PART-D (VI. Answer any three of the following questions.) |5 VideosSUPPLEMENTARY EXAM QUESTION PAPER JULY - 2014
SUNSTAR PUBLICATION|Exercise PART-D (IV. Answer any two of the following questions.) |3 VideosP.U. BOARD LATEST MODEL QUESTION PAPER-3
SUNSTAR PUBLICATION|Exercise PART-D|11 VideosSUPPLEMENTARY EXAM QUESTION PAPER JULY -2015
SUNSTAR PUBLICATION|Exercise PART-D|11 Videos
Similar Questions
Explore conceptually related problems