Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MAXIMUM PUBLICATION-PARALLEL LINES-EXAMPLE
- Draw a line of length 8 cm divide it in the ratio 2:1
Text Solution
|
- Draw a rectangle of perimeter 15 cm and sides are in the 3:4.
Text Solution
|
- Draw a tiangle specified below, perimeter 10 cm. Equilatral triangle...
Text Solution
|
- Draw a tiangle specified below, each of perimeter 10 cm. side in the...
Text Solution
|
- Draw a tiangle specified below, each of perimeter 10 cm. Sides in th...
Text Solution
|
- In the picture below, the diagonals of the trapezium ABCD intersect at...
Text Solution
|
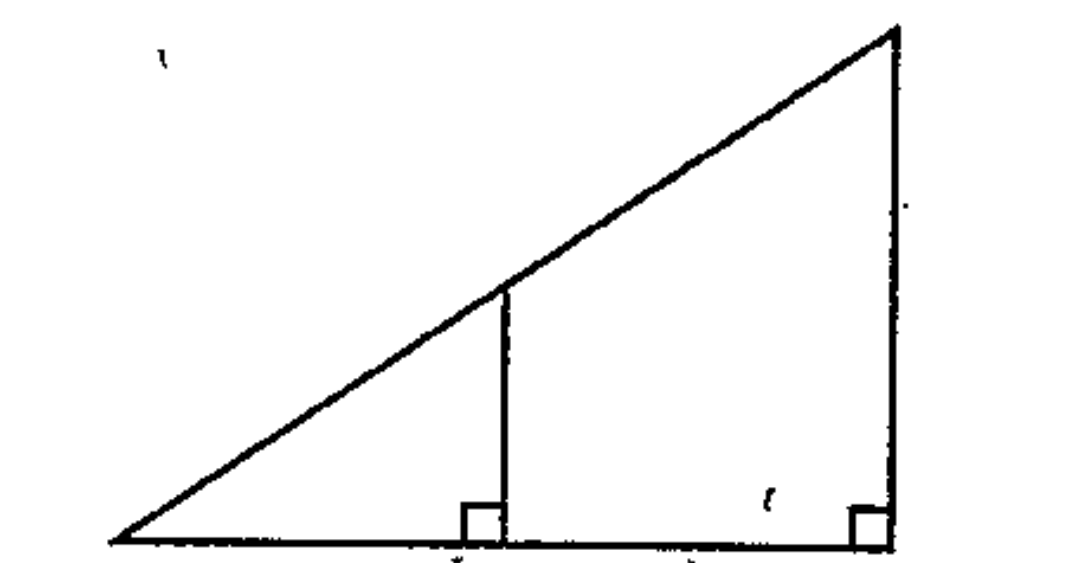
- Draw a right triangle and the perpendicular from the midpoint of the o...
Text Solution
|
- Draw a right triangle and the perpendicular from the midpoint of the o...
Text Solution
|
- Draw a right triangle and the perpendicular from the midpoint of the o...
Text Solution
|
- Draw a right triangle and the perpendicular from the midpoint of the o...
Text Solution
|
- In the parallelogram ABCD, the line drawn through Q point P on AB, par...
Text Solution
|
- In the picture below, two vertices of a parallelogram are joined to th...
Text Solution
|
- Prove that the quadrilatral formed by joining the mid points of the si...
Text Solution
|
 .
.