Similar Questions
Explore conceptually related problems
MAXIMUM PUBLICATION-SIMILAR TRIANGLES-EXAMPLE
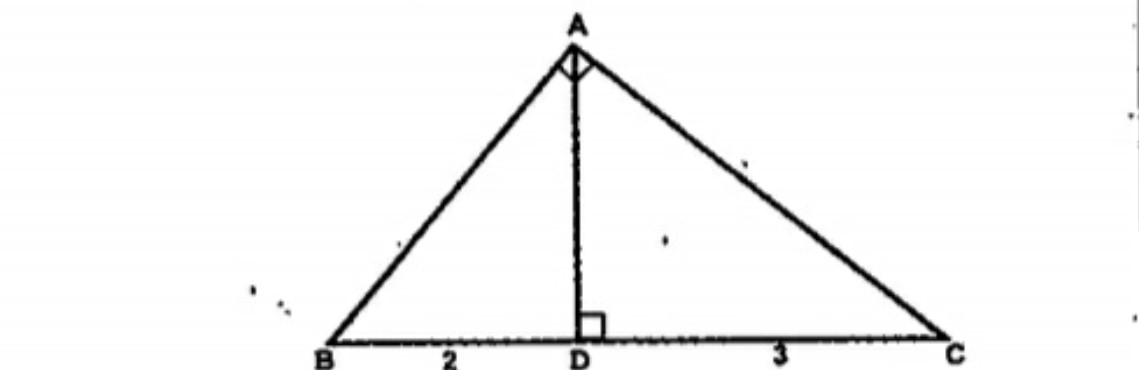
- The perpendicular from the square corners of a right angle triangle cu...
Text Solution
|
- The perpendicular from the square corners of a right angle triangle c...
Text Solution
|
- The perpendicular from the square corners of a right angle triangle cu...
Text Solution
|
- The perpendicular from the square comers of a right triangle cuts the ...
Text Solution
|
- At two ends of a horizontal line, angles of equal size are drawn, and...
Text Solution
|
- At two ends of a horizontal line, angles of equal size are drawn, and ...
Text Solution
|
- At two ends of a horizontal line, angles of equal size are drawn, and ...
Text Solution
|
- The picture shows a square drawn sharing one cor¬ner with a right tria...
Text Solution
|
- Two poles of height 3 m and 2m are erected upright on the ground and r...
Text Solution
|
- Two poles are erected upright on the ground and ropes are stretched fr...
Text Solution
|
- Two poles of height 3 m and 2m are erected upright on the ground and r...
Text Solution
|
- The picture shows two circles with the same centre and two triangles f...
Text Solution
|
- The lines joining the circumcentre of a Wangle to the vertices are ext...
Text Solution
|
 .
.