Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRUCTURAL ORGANISATION IN ANIMALS
ICSE|Exercise Test Your Progress (Very Short Answer Type Questions )|64 VideosSTRUCTURAL ORGANISATION IN ANIMALS
ICSE|Exercise Test Your Progress (Short/Long Answer Type Questions )|35 VideosSTRUCTURAL ORGANISATION IN ANIMALS
ICSE|Exercise Test Your Progress (Fill in the blanks with appropriate words) |20 VideosSELF ASSESSMENT PAPER-3
ICSE|Exercise PART II (SECTION C)|4 VideosSTRUCTURE ORGANISATION IN ANIMALS -ANIMAL TISSUES
ICSE|Exercise REVIEW QUESTIONS (LONG ANSWER TYPE QUESTIONS)|12 Videos
Similar Questions
Explore conceptually related problems
ICSE-STRUCTURAL ORGANISATION IN ANIMALS -Test Your Progress (State whether the following statements are true or false )
- Adjacent epithelial cells are held together by desmosomes.
Text Solution
|
- A tendon joins muscle to muscle.
Text Solution
|
- Unstriped muscles are always voluntary in nature.
Text Solution
|
- Pseudo-stratified epithelium is found in the mucous membrane of trach...
Text Solution
|
- Stratified squamous epithelium covers moist surfaces like buccal cavi...
Text Solution
|
- All glands, whether exocrine or endocrine in a mammal, originate from...
Text Solution
|
- Keel is the characteristic feature of flower of :
Text Solution
|
- Fibroblasts store fat in the adipose tissue.
Text Solution
|
- Gravitational potential at a height R from the surface of the earth wi...
Text Solution
|
- Single-unit smooth muscle fibres may contract automatically and rhyth...
Text Solution
|
- In a complimentary gene interaction calculate the number of phenotype ...
Text Solution
|
- In cockroach, the malpighian tubules constitute the excretory system.
Text Solution
|
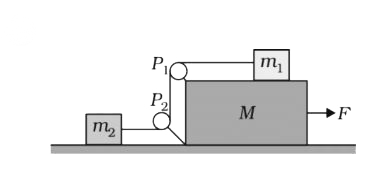
- In the figure, masses m(1), m(2) and M are 20kg, 5kg, and 50kg respect...
Text Solution
|
- The respiratory system of cockroach is very well developed and consis...
Text Solution
|
- The leaves are modified into spines in
Text Solution
|