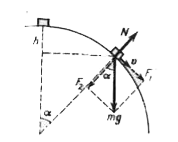
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A small disk of mass m lies on the highest point of a sphere of radius...
Text Solution
|
- Two disks of masses m(1) and m(2) are connected by a spring of force c...
Text Solution
|
- A unifrom solid disk of radius R and mass M is free to rotate on a fri...
Text Solution
|
- A solid unifrom disk of mass m and radius R is pivoted about a horizon...
Text Solution
|
- A uniform solid disk rolling down an incline making angle theta with t...
Text Solution
|
- A mass m is attached to a pulley through a cord as shown in figure. Th...
Text Solution
|
- A solid uniform disk of mass m rolls without slipping down a fixed inc...
Text Solution
|
- A disk and a sphere roll off two inclined planes of the same altitude ...
Text Solution
|
- a. किसी गोले का इसके किसी व्यास के परितः जड़त्व-आघूर्ण 2MR^(2)//5 है जह...
Text Solution
|