Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
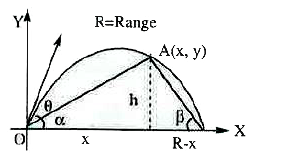
- A particle is thrown over a triangle from one end of a horizontal base...
Text Solution
|
- A particle is thrown over a triangle from one end of a horizontal base...
Text Solution
|
- A particle is projected over a triangle from one extremity of its hori...
Text Solution
|
- A particle is projected over a traingle from one end of a horizontal b...
Text Solution
|
- A projectile is fired from the base of cone shaped hill. The projectle...
Text Solution
|
- A particle thrown over a triangle from one end of a horizontal base fa...
Text Solution
|
- सिद्ध कीजिए कि किसी त्रिभुज के एक आधार कोण के अन्तः अर्धक तथा दूसरे आध...
Text Solution
|
- समद्विबाहु त्रिभुज की बराबर भुजाओं में से एक को आधार के सम्मुख शीर्ष क...
Text Solution
|
- सिद्ध कीजिए कि एक त्रिभुज के एक आधार कोण के अन्तः समद्विभाजक तथा दूसरे...
Text Solution
|