Home
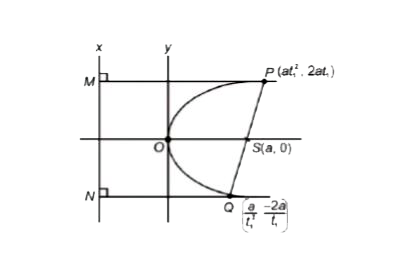
Class 11
MATHS
If and k are segments of a focal chord o...

If and k are segments of a focal chord of the parabola `y^(2)= 4ax`, then k =

A

`(b+c)/(2)`

B

`(bc)/(b+c)`

C

`(2bc)/(b+c)`

D

`sqrt(bc)`

Text Solution

Verified by Experts

The correct Answer is:
C

Let `P(at_(1)^(2), 2at_(1)) and Q (at_(2)^(2), 2at_(2))` are end points of a chord
PQ is a focal chord
`t_(1)t_(2)= -1`
`t_(2)= (-1)/(t_(1))`
`Q((a)/(t_(1)^(2)), (-2a)/(t_(1)))`
`b=SP=PM=a+at_(1)^(2)`
`b-a=at_(1)^(2) ...........(i)`
`c= SQ=QN=a+(a)/(t_(1)^(2))`
`c-a=(a)/(t_(1)^(2)) ...........(ii)`
Promotional Banner

Similar Questions

Explore conceptually related problems

If b and k are segments of a focal chord of the parabola y^(2)= 4ax , then k =

The Harmonic mean of the segments of a focal chord of the parabola y^(22)=4ax is

If b and c are lengths of the segments of any focal chord of the parabola y^(2)=4ax, then write the length of its latus rectum.

The harmonic mean of the segments of a focal chord of the parabola y^(2)=16ax, is

AB is a focal chord of the parabola y^(2)=4ax If A=(4a,4a) then B=

If 't_1' and 't_2' be the ends of a focal chord of the parabola y^2=4ax then t_1t_2 is equal to

If b and c are the lengths of the segments of any focal chord of a parabola y^(2)=4ax , then length of the semi-latus rectum is:

If a and c are lengths of segments of focal chord of the parabola y^(2)=2bx (b>0) then the a,b,c are in