Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
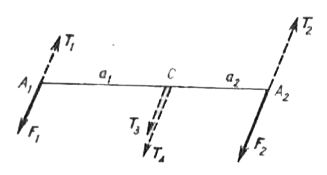
- Applying to the system two force couples having torques equal in magni...
Text Solution
|
- For what value of m the roots of the equation I are equal in magnitude...
Text Solution
|
- If roots of ax^(2)+bx+c=0 are equal in magnitude but opposite in sign,...
Text Solution
|
- A horizontal force F is applied such that the block remains stationary...
Text Solution
|
- The ............ on a proton is equal in magnitude but opposite in sig...
Text Solution
|
- If the zeroes of quadratic polynomial are equal in magnitude but oppos...
Text Solution
|
- IF the roots of ax^2+bx +c=0 are equal in magnitude but opposit...
Text Solution
|
- किन्हीं दो पिंडों के बीच लगने वाले गुरुत्वाकर्षण बल परिमाण में बराबर औ...
Text Solution
|
- If the roots of ax^(2)+ bx + c = 0 are equal in magnitude but opposite...
Text Solution
|