Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
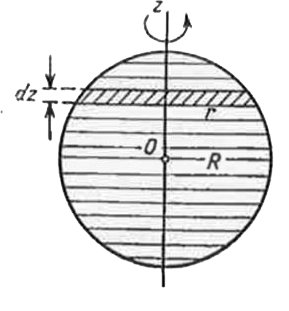
- Derive, making use of an integral, the formula for the moment of inert...
Text Solution
|
- The moment of inertia of a soild sphere about a tangent is (5)/(3)mr^(...
Text Solution
|
- What is moment of inertia of a solid sphere about its diameter ?
Text Solution
|
- एक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है। इस गोले का अपने व्यास क...
Text Solution
|
- If temperature increases, the moment of inertia of a solid sphere abou...
Text Solution
|
- Moment of inertia of a solid sphere about its diameter is I . If that ...
Text Solution
|
- The moment of inertia of a solid sphere of mass M and radius R about i...
Text Solution
|
- किसी ठोस गोले का उसके व्यास के सापेक्ष जड़त्व आघूर्ण का मान 1 है तो गोल...
Text Solution
|
- Find the moment of inertia of a sphere about a tangent to the sphere. ...
Text Solution
|