Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
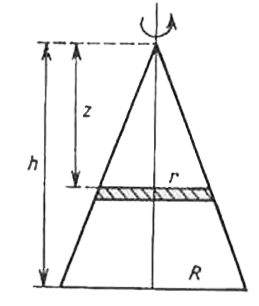
- Derive, making use of an integral, the formula for the moment of inert...
Text Solution
|
- Derive an expression for moment of inertia of a thin circular ring abo...
Text Solution
|
- The radius of base and height of a right circular cone are equal . If...
Text Solution
|
- The moment of inertia of a circular dics about one of its diameters is...
Text Solution
|
- Derive the expresssion for moment of inertia of a rod about its centre...
Text Solution
|
- Derive the volume of a cone using integration.
Text Solution
|
- Derive the formula for the volume of right circular cone with radius r...
Text Solution
|
- The moment of inertia of a Thin rod about and axis passing through the...
Text Solution
|
- Derive the expresssion for moment of inertia of a rod about its centre...
Text Solution
|