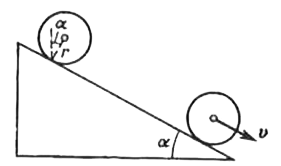
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A solid cylinder with base radius jis placed on top of an inclined pla...
Text Solution
|
- A cylinder of radius R and mass M rolls without slipping down a plane ...
Text Solution
|
- A solid cylinder is rolling down on an inclined plane of angle theta. ...
Text Solution
|
- A solid cylinder of mass m rolls without slipping down an inclined pla...
Text Solution
|
- The least coefficient of friction for an inclined plane inclined at an...
Text Solution
|
- Derive an expression for the acceleration of a solid cylinder rolling ...
Text Solution
|
- The least coefficient of friction for an inclined plane inclined at an...
Text Solution
|
- एक ठोस बेलन theta कोण पर झुके नत समतल पर नीचे की ओर लुढ़कता है। समतल ...
Text Solution
|
- A solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane...
Text Solution
|