Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-CIRCULAR MOTION -MODULE 2 (FROM ANGULAR MOMENTUM - CONSERVATION)
- A car of mass 1000 kg moves on a circular track of radius 100 m with a...
Text Solution
|
- A uniform sphere of radius 0.25 m and mass 2 kg rotates about its diam...
Text Solution
|
- The mean distance of the moon from the earth is 3.84 xx 10^5 km and it...
Text Solution
|
- A particle of-mass m moves along a circular path of radius r with velo...
Text Solution
|
- Find the angular momentum of a satellite of mass m moving round the ea...
Text Solution
|
- Locate ,the centre of mass of the uniform then L-shaped body as shown ...
Text Solution
|
- Two particles of masses m1 and m2 are joined by a light rigid rod of l...
Text Solution
|
- If m(1) = 3 kg and m2 = 1 kg what is the angular momentum of the syst...
Text Solution
|
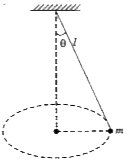
- Fig. show a conical pendulum. If the length of the pendulum is l, mass...
Text Solution
|
- A small body of mass 100 g moving with a velocity 2 m/s is strikes a s...
Text Solution
|
- The torque acting on a particle about an arbitrary origin is zero, wha...
Text Solution
|
- If earth suddenly contracts by 1/2 of its present radius by how much w...
Text Solution
|
- The maximum and minimum distances of a cornet form Sun are 1.4 xx 10^(...
Text Solution
|
- The mass ofa star is 3.98 xx 10^30 kg and its radius is 106 km. It rot...
Text Solution
|