Home
Class 10
PHYSICS
The wheel shown in the diagram (Fig.1.18...

The wheel shown in the diagram (Fig.1.18) has a fixed axle passing through O. The wheel is kept stationary under the action of (i) a horizontal force `F_1` at A and (ii) a vertical force `F_2` at B.
(a) Show the direction of force `F_2` in the diagram.
(ii) Which of the force `F_1 or F_2` is greater
(c) Find the ratio between the forces `F_1 and F_2` Given: AO =2.5 cm
BO'=1.5 cm and O'O=2.0cm

Text Solution

Verified by Experts

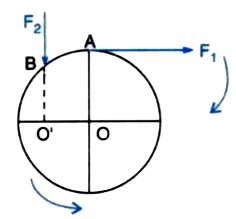
The force `F_1` applied at A produces a clockwise moment on the wheel. It can be balanced by applying the force `F_2` at B in a direction such that it produces an anticlockwise moment. Therefore the vertical force at B should be applied in the downward direction as shown in FIg.1.19 In equilibrium `F_1 times OA=F_2 times OO.`
(b) SInce the perpendicular forces `F_1` from O is greater than the perpendicular distance OO. of point of application of force `F_2` from O, so in magnitude, force `F_2` is greater than force `F_1`
(c) Moment of force `F_1` about `O= F_1 times OA` (clockwise )
Moment of force `F_2` about `O=F_2 times OO.` (anticlockwise)
When the wheel is in equilibrium position,
Clockwise moment= Anticlockwise moment
i.e., `F_1 times OA=F_2 times OO.`
`therefore F_2/F_1= (OA)/(OO.)`........(i)
Given OA=2.5 cm and OO.=2.0 cm
Substituting the values of OA and OO. in eqn. (i), the ratio of forces
`F_2/F_1=2.5/2.0 or F_2:F_1=5:4`
Promotional Banner

Topper's Solved these Questions

  • FORCE

    ICSE|Exercise EXERCISE 1A|27 Videos

  • FORCE

    ICSE|Exercise EXERCISE 1(A) Multiple choice questions|2 Videos

  • ELECTRO-MAGNETISM

    ICSE|Exercise EXERCISE-10 (C) NUMERICALS |1 Videos

  • HOUSEHOLD CIRCUITS

    ICSE|Exercise EXERCISE -9(B) (MULTIPLE CHOICE TYPE)|2 Videos

Similar Questions

Explore conceptually related problems

Two forces F_(1) " and " F_(2) are acting on a rod abc as shown in figure.

Two force F_(1)" and "F_(2) are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is :-

Two forces F_(1) and F_(2) are acting on a body. One force is double that of the other force and the resultant is equal to the greater force. Then the angle between the two forces is

A block of mass m is taken from A to B under the action of a constant force F. Work done by this force is

The diagram in Fig.1.29 shows two forces F_1=5N and F_2=3N acting at points A and B of a rod pivoted at a point O, such that OA=2m and OB=4m Calculate: (i) the moment of force F_1 about O. (ii) the moment of force F_2 about O. (iii) total moment of the two forces about O.

A body is at rest under the action of three forces, two of which are vec(F)_(1)= 4hat(i), vec(F)_(2)= 6hat(j) , the third force is

If in pervious problem, an additional force F' = 100N is applied in vertical direction as shown in figure The friction force acting on the block is

A force F_1 acts on a particle so as to accelerate it from rest to a velocity v. The force F_1 is then replaced by F_2 which decelerates it to rest

Consider the situations of the previous proble. Let the water push the left wass by a force F_1 and the right wall byi as force F_2 .

A force F_1 acts on a particle so as to accelerate it from rest to a velocity v. The force F_1 is then replaced by F_2 which decelerates it to rest.