Similar Questions
Explore conceptually related problems
Recommended Questions
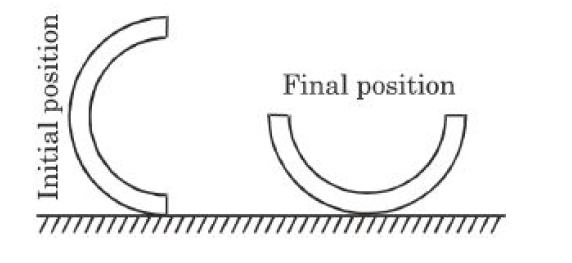
- A half section of thin circular pipe of mass m and radius 'r' is relea...
Text Solution
|
- A solid cylinder C and a hollow pipe P of same diameter are in contact...
Text Solution
|
- A long thin walled pipe of radius R carries a current I along its leng...
Text Solution
|
- A particle of mass 'm' is rigidly attached at 'A' to a ring of mass 3m...
Text Solution
|
- A particle of mass m oscillates inside the smooth surface a fixed pipe...
Text Solution
|
- A solid cylinder C and a hollow pipe P of same diameter are in contact...
Text Solution
|
- A ring of radius R is rolling purely on the outer surface of a pipe of...
Text Solution
|
- Soap bubble of radius R is blown at one end of a pipe of circular of c...
Text Solution
|
- Soap bubble of radius R is blown at one end of a pipe of circular of c...
Text Solution
|