Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-UNDERSTANDING SHAPES-Exercise 16C
- Two angles of a quadrilateral are 89^@ and 113^@. If the two angles ar...
Text Solution
|
- Two angles of a quadrilateral are 68^@ and 76^@. If the other two angl...
Text Solution
|
- Angles of a quadrilateral are (4x)^@, 5(x+2)^@, (7x-20)^@ and 6(x+3)^@...
Text Solution
|
- Use of the information given in the following figure to find: (i) x ...
Text Solution
|
- In quadrilateral ABCD, side AB is parallel to side DC. If angleA : ang...
Text Solution
|
- From the following figure, find (i) x (ii) angleABC (iii) angleA...
Text Solution
|
- Given : In quadrilateral ABCD, angleC= 64^@, angleD= angleC-8^@, angle...
Text Solution
|
- In the given figure : angleb=2a+15^@ and anglec=3a+5^@, find the value...
Text Solution
|
- Three angles of a quadrilateral are equal. If the fourth angle is 69^@...
Text Solution
|
- In quadrilateral PQRS, angleP: angleQ: angleR: angleS= 3:4:6: 7. Calcu...
Text Solution
|
- Use the information given in the following figure to find the value of...
Text Solution
|
- The following figure shows a quadrilateral in which sideo AB and DC ar...
Text Solution
|
- Use the following figure to find the value of x.
Text Solution
|
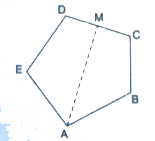
- ABCDE is a regular pentagon. The bisector of angle A of the pentagon m...
Text Solution
|
- In a quadrilateral ABCD, AO and BO are bisector of angle A and angle B...
Text Solution
|