Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-AREA THEOREMS-Exercies 16(B)
- Show that : (i) a diagonal divides a parallelogram into two triangle...
Text Solution
|
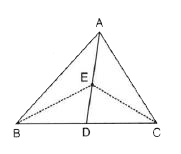
- In the given figure, AD is median of DeltaABC and E is any point on me...
Text Solution
|
- In the figure of question 2, if E is the mid point of median AD, then ...
Text Solution
|
- ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD...
Text Solution
|
- The base BC of triangle ABC is divided at D so that BD = (1)/(2) DC. ...
Text Solution
|
- In a parallelogram ABCD, point P lies in DC such that DP:PC= 3:2. If a...
Text Solution
|
- ABCD is a parallelogram in which BC is produced to E such that CE=BC a...
Text Solution
|
- The following figure shows a triangle ABC in which P, Q and R are mid-...
Text Solution
|
- Show that : (i) a diagonal divides a parallelogram into two triangle...
Text Solution
|
- In the given figure, AD is median of DeltaABC and E is any point on me...
Text Solution
|
- In the figure of question 2, if E is the mid point of median AD, then ...
Text Solution
|
- ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD...
Text Solution
|
- The base BC of triangle ABC is divided at D so that BD = (1)/(2) DC. ...
Text Solution
|
- In a parallelogram ABCD, point P lies in DC such that DP:PC= 3:2. If a...
Text Solution
|
- ABCD is a parallelogram in which BC is produced to E such that CE=BC a...
Text Solution
|
- The following figure shows a triangle ABC in which P, Q and R are mid-...
Text Solution
|