Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
ICSE-CIRCLE-EXERCISE 17(B)
- The figure shows two concentric circles and AD is a chord of larger ci...
Text Solution
|
- A straight line is drawn cutting two equal circles and passing through...
Text Solution
|
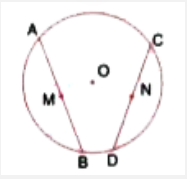
- M and N are the mid-points of two equal chords AB and CD respectively ...
Text Solution
|
- M and N are the mid-points of two equal chords AB and CD respectively ...
Text Solution
|
- In the following figure, P and Q are the points of intersection of two...
Text Solution
|
- In the following figure, P and Q are the points of intersection of two...
Text Solution
|
- Two equal chords AB and CD of a circle with centre O, intersect each o...
Text Solution
|
- Two equal chords AB and CD of a circle with centre O, intersect each o...
Text Solution
|
- In the following figure, OABC is a square. A circle is drawn with O as...
Text Solution
|
- In the following figure, OABC is a square. A circle is drawn with O as...
Text Solution
|
- The length of common chord of two intersecting circles is 30 cm. If th...
Text Solution
|
- The line joining the mid-points of two chords of a circle passes throu...
Text Solution
|
- In the following figure, the line ABCD is perpendicular to PQ, where P...
Text Solution
|
- In the following figure, the line ABCD is perpendicular to PQ, where P...
Text Solution
|
- AB and CD are two equal chords of a circle with centre O which interse...
Text Solution
|