Home
Class 12
PHYSICS
Two bodies with masses m(1) and m(2) gt ...

Two bodies with masses `m_(1)` and `m_(2) gt m_(1)` connected by a thread lie on a smooth table. A force Q is first applied to the larger and then to the smaller of the bodies (Fig.). Is the tension of the thread in both cases the same?

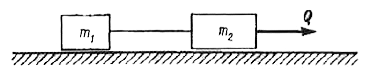
Text Solution

Verified by Experts

The correct Answer is:
It is greater in the second case.

The equations of motions for the case shown in Fig. are of the form
`Q-F_(1)= m_(2)a, F_(1)=m_(1)a`
from which we get
`F_(1)= Q m_(1)//(m_(1)+m_(2))`
If the force is applied to the smaller body, the string tension would become
`F_(2)= Q m_(2)// (m_(1)+m_(2)) gt F_(1)`
Promotional Banner

Similar Questions

Explore conceptually related problems

Two bodies with masses m_1 and m_2 (m_2 gt m) connected by a thread lie on a smooth table. A force Q is first applied to the larger mass and then to the smaller mass. The ratio of tensions in the thread in the two cases will be

Two bodies of masses m_1 and m_2(

Two bodies of masses m_(1) and m_(2) have same kinetic energy. The ratio of their momentum is

There blocks of masses m_(1) , m_(2) and m_(3) are connected by may less unstretchable strings on a smooth surface. Tension T_(2) is.

Two blocks of masses '3m' and '2m' are in contact on a smooth table. A force P is first applied horizontally on block of mass '3m' and then on mass '2m'. The contact forces between the two blocks in the two cases are in the ratio?

Two bodies of masses m_(1)and m_(2) are connected by a non-deformed light speing and lie on a horizontal plane. Coefficient of friction between the surface and the blocks is mu. Find an expression for the work done by the various foeces. Force F is applied horzontally to body of mass m_(1) in order to shift body of mass m_(2).

Two bodies of masses m_(1) and m_(2) are separated by a distance R. The distance of the centre of mass of the bodies from the mass m_(1) is

Consider the case of two bodies of masses m_(1) and m_(2) which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations: (i) when m_(1) gt m_(2) . In this case a=((m_(1)-m_(2))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (ii) when m_(2) gt m_(1) . In this case a=((m_(2)-m_(1))/(m_(1)+m_(2)))g and T=((2m_(1)m_(2))/(m_(1)+m_(2)))g (iii) When m_(1)=m_(2)=m . In this case a = 0, T = mg What is the tension in the string?