Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
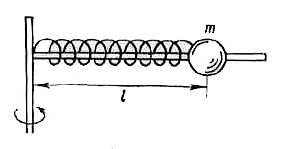
- An underformed spring with the spring constant k has length l(0). When...
Text Solution
|
- A block of mass 'm' is attached to a spring in natural length of sprin...
Text Solution
|
- A particle of mass m is fixed to one end of a massless spring of sprin...
Text Solution
|
- If the system is suspended by the mass m the length of the spring is l...
Text Solution
|
- A particles of mass m is fixed to one end of a light spring of force c...
Text Solution
|
- In a spring- mass system , the length of the spring is L, and it has a...
Text Solution
|
- The block of mass m is released when the spring was in its natrual len...
Text Solution
|
- A mass m attached to spring of natural length l0 and spring constant k...
Text Solution
|
- A particles of mass m is fixed to one end of a light spring of force c...
Text Solution
|