Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
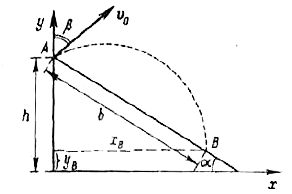
- The surface of a hill is inclined at an angle alpha to the horizontal ...
Text Solution
|
- A stone is thrown by a student from the bottom of a hill with a veloci...
Text Solution
|
- The surface of a hill is inclined at an angle alpha to the horizontal....
Text Solution
|
- The surface of a hill is inclined at an angle alpha to the horizontal ...
Text Solution
|
- From a point on a hillside of constant inclination , the angle of elev...
Text Solution
|
- एक पहाड़ी का ढ़लान क्षितिज से 60^(@) का कोण बनता है। यदि शिखर तक पहुं...
Text Solution
|
- एक पहाड़ी का ढ़लान क्षैतिज से 30^(@) कोण बनाता है। यदि शिखर तक पहुंचने...
Text Solution
|
- Angle of elevation of hill top from the base of a tower 60^(@) And the...
Text Solution
|
- एक पत्थर को किसी पहाड़ी के शीर्ष से फेंका जाता है तथा n सेकण्ड के बाद,...
Text Solution
|