The coefficient of friction between the block and the inclined plane is `mu`.

Answer

`a="g"(m-M(sin alpha pm mu cos alpha))/(m+M)`

Explanation

Since the force of sliding friction T is opposite in direction to that of the block.s motion, the result will be essentially dependent on the initial direction of the block velocity. Consider all the possible cases.
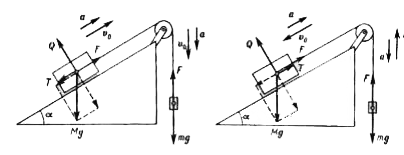
Let the initial velocity of teh weight be directed downwards (Fig.). The equations of motion will be of the form
`mg - F = ma`
`F-T-Mg sin alpha= Ma`, where `T= muQ=muMg cos alpha`
Hence
`a= "g"(m-M(sin alpha +mu cos alpha))/(m+M) , F=(mMg(1+sin alpha +mu cos alpha))/(m+M)`
If `m gt M (sin alpha + mu cos alpha)`, then `a gt 0` and the speed of the system increases. If `m lt M (sin alpha +mu cos alpha)`, then `a lt 0`, and the speed

of the system decreases. Lastly, when `m=M(sin alpha +mu cos alpha)`, we have a = 0, and the system moves at a constant speed.
(2) Let the initial velocity of the weight be directed upwards (Fig.). Then, as may easily be inferred,
`a="g"(m-M(sin alpha - mu cos alpha))/(m+M), F= (mMg(1+sin alpha- mu cos alpha))/(m+M)`
If `m gt M(sin alpha- mu cos alpha)`, then `a gt 0`, and the speed of the system decreases. If `m lt M(sin alpha - mu cos alpha)`, then `a lt 0`, and the speed of the system moves at a constant speed.
(3) Finally, let the system be at rest. Then a force of static friction will act between the block and the inclined plane, its direction being dependent on the direction in which the system would move in the absence of friction. If `m gt M sin alpha`, the block in th absence of friction moves upwards. Therefore the force of static friction is directed downwards, as in Fig. If `m lt M sin alpha`, the block in the absence of friction moves downwards, and for this reason the force of static friction is directed upwards, as in Fig.
If one analyses the two preceding cases, one can easily see that for `m gt M (sin alpha +mu cos alpha)` the black will move up the inclined plane with an acceleration, for `m lt M(sin alpha- mu cos alpha)` it will move down the inclined plane with an acceleration, will for
`M (sin alpha- mu cos alpha) le m le M(sin alpha+mu cos alpha)`
the system will remain at rest.