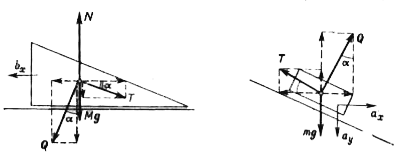
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The coefficient of friction between the block and the wedge is mu. Fri...
Text Solution
|
- If the coefficient of friction between A and B is mu, the maximum acce...
Text Solution
|
- The coefficient of friction between the block A of mass m and the tria...
Text Solution
|
- A block of mass m is at rest relative to the stationary wedge of mass ...
Text Solution
|
- Calculate angle of friction between wedge and block system is at rest ...
Text Solution
|
- Two small blcok m=2kg each kept on wedge of mass 12 kg . There is no f...
Text Solution
|
- a Block of mass m is placed on a wedge of mass M there is no friction ...
Text Solution
|
- Coefficient of friction between block of mass m and fixed wedge is mu ...
Text Solution
|
- A block on table shown in figure is just on the wedge of slipping. Fin...
Text Solution
|