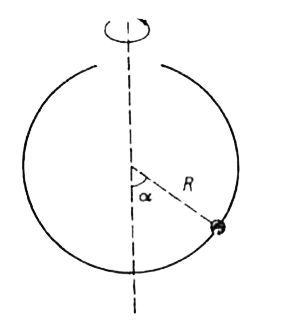
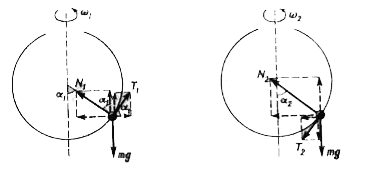Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A spherical bowl of radius R rotates about the vertical diameter. The ...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- A block is kept inside a hemispherical bowl rotating with angular velo...
Text Solution
|
- A spherical bowl of radius R rotates about the verical diameter with a...
Text Solution
|
- द्रव्यमान m की एक वस्तु त्रिज्या R वाले अर्द्धगोलीय प्याले के धरातल पर...
Text Solution
|
- A hemispherical bowl of radius r is rotated with an angular velocity o...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|
- A hemispherical bowl of radius R is set rotating about its axis of sym...
Text Solution
|