Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
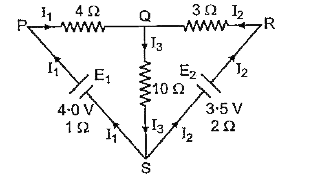
- In the circuit shown in figure below, E(1) and E(2) are batteries havi...
Text Solution
|
- In the circuit shows in Fig E = 15 V, R(1) = 1Omega, R(2) = 1 Omega, R...
Text Solution
|
- In the circuit shown below E(1) = 4.0 V, R(1) = 2 Omega, E(2) = 6.0 V,...
Text Solution
|
- In the circuit shown in the figure, the switch S is initially open and...
Text Solution
|
- A battery of emf epsilon and internal resistance r sends currents I(1)...
Text Solution
|
- Compute the values of i(1),i(2),i(3) and V in the circuit, shown in fi...
Text Solution
|
- In the circuit shown in figure. Find the currents I,I(1),I(2) and I(3)...
Text Solution
|
- If the resistances are chosen for the circuit shown in figure in such ...
Text Solution
|
- In the circuit shown, E(1)= 7 V, E(2) = 7 V, R(1) = R(2) = 1Omega and ...
Text Solution
|