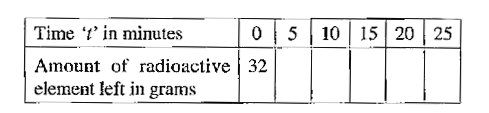Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
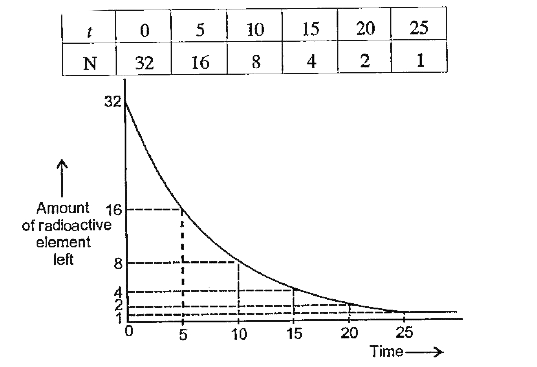
- Complete the following table for a radioactive element whose half life...
Text Solution
|
- A radioactive nulei has half-life of 1.0 minute. If one of the nuclie ...
Text Solution
|
- A radioactive element has half life of 30 seconds. If one of the nucle...
Text Solution
|
- Consider a radioactive material of half-life 1.0 minute. If one of the...
Text Solution
|
- The half-life of a radioactive element is 100 minutes . The time inte...
Text Solution
|
- The half life period of a radioactive element is 90 minutes. What perc...
Text Solution
|
- The t(0.5) of a radioactive element is related to its average life by ...
Text Solution
|
- The half life of 1 gm of a radioactive element of atomic weight M is T...
Text Solution
|
- Radioactive element has a half life of 25 minutes. Calculate the fract...
Text Solution
|