Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
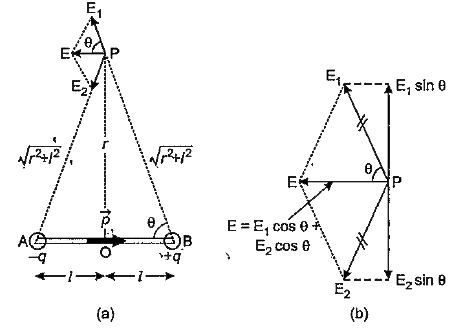
- Derive an expression for intensity of electric field are a point in br...
Text Solution
|
- Electric Field Intensity Due To An Electric Dipole At A Point On The E...
Text Solution
|
- Derive an expression for the intensity of the electric field at a poin...
Text Solution
|
- Derive an expression for the intensity of the electric field at a poin...
Text Solution
|
- Derive the expression for electric fiedl at a point on the equatorial ...
Text Solution
|
- Define electric dipole moment. Is it a scalar or a vector ? Derive the...
Text Solution
|
- Derive a relation for electric field of an electric dipole at a point ...
Text Solution
|
- Derive an expression for electric field intensity of a point on the eq...
Text Solution
|
- Derive an expression for the electric field it a point on the equatori...
Text Solution
|