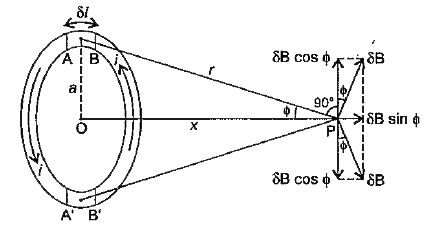
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Obtain an expression for magnetic flux density B at the centre of a ci...
Text Solution
|
- A circular coil of radius 25cm , carries a current of 50 ampere. If it...
Text Solution
|
- The magnetic moment of a current (i) carrying circular coil of radius ...
Text Solution
|
- A circular coil of radius 'r' having N turns carries a current ''I''. ...
Text Solution
|
- A circular coil of closely wound N turns and radius r carries a curren...
Text Solution
|
- A circular coil of radius r having number of turns n and carrying a cu...
Text Solution
|
- The magnetic moment of a current (i) carrying circular coil of radius ...
Text Solution
|
- State the expression for the magnetic field due to a circular are of w...
Text Solution
|
- A circular coil of n turns and radius r carries a current I. The magne...
Text Solution
|