Home
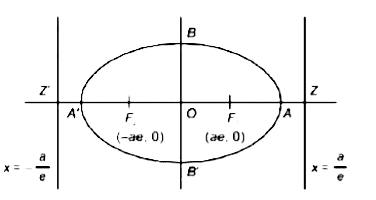
Class 11
MATHS
In an ellipse the distance between the f...

In an ellipse the distance between the foci is 8 and the distance between the directrices is 25, then the ratio of the length of major and minor axis is

A

`(5)/(sqrt(17))`

B

`(3)/(sqrt(17))`

C

`(4)/(sqrt(17))`

D

`(6)/(sqrt(17))`

Text Solution

Verified by Experts

The correct Answer is:
A
Given `F_(1)F_(2)=8 rArr 2a e=8 rArr ae = 4 `
Also, `Z Z'=25`
`rArr (2a)/(e )=25`
`rArr (2a)/((4)/(a))=25" " e=(4)/(a)`
`rArr 2a^(2)=25xx4=100 =(4)/(5sqrt(2))`

`rArr a^(2)=50`
`rArr a=5sqrt(2)`
`:.b^(2)=a^(2)(1-e^(2)) " Ratio"=(5sqrt(2))/(sqrt(34))`
`=50(1-(16)/(50)) " " =(5)/(sqrt(17))`
`=(50)/(50)xx34`
`rArr b=sqrt(34)`
Promotional Banner

Similar Questions

Explore conceptually related problems

In an ellipse the distance between the foci is 8 and the distance between the directrices is 25. The length of major axis, is

Distance between foci is 4 and distance between directrices is 5

In an ellipse the distance between the foci is 8 and the distance between the directrices is 25. The length of major axis is : (A) 5sqrt(2) (B) 10sqrt(2) (C) 20sqrt(2) (D) none of these

Find the equation of an ellipse the distance between the foci is 8 units and the distance between the directrices is 18 units.

If the distance foci of an ellipse is 8 and distance between its directrices is 18 , then the equation of the ellipse is

Distance between foci is 8 and distance between directrices is 6 of hyperbola, then length of latusrectum is

If distance between foci = 3 (distance between directrices) . Then e =

If distance between the foci of an ellipse is 6 and distance between its directionces is 12, then length of its latus rectum is

Can the distance between foci of an ellipse be equal to distance its directrices ?