Similar Questions
Explore conceptually related problems
Recommended Questions
- Using Gauss’s law, derive expression for intensity of electric field a...
Text Solution
|
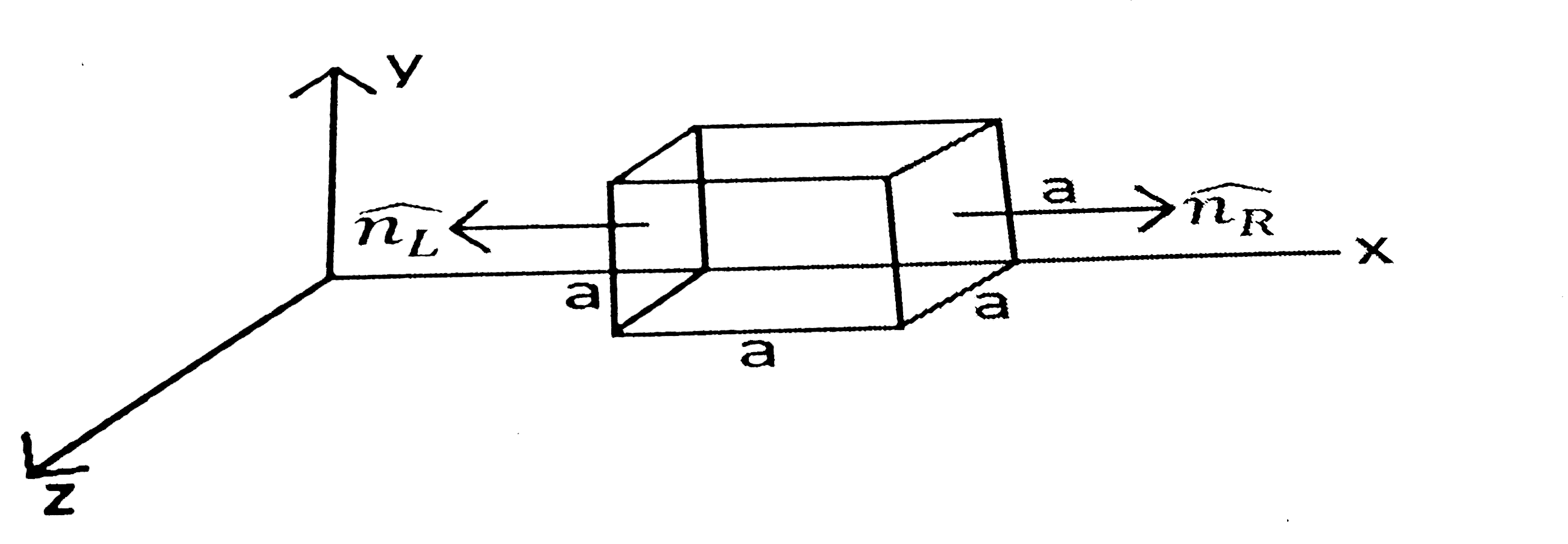
- The electric field componets due to a charge inside the cube of side ...
Text Solution
|
- The electric components in the figure are E(x)=alphax^(1//2) ,E(y)=0,E...
Text Solution
|
- Due to a charge inside the cube, the electric field is: E(x) = 600x, E...
Text Solution
|
- Using Gauss’s law, derive expression for intensity of electric field a...
Text Solution
|
- Define electric flux and write its SI unit . The electric field compon...
Text Solution
|
- 0.1m भुजावाले एक गहन के भीतर विधुत-क्षेत्र के घटक चित्र में दिखाए गए ह...
Text Solution
|
- Using Gauss’ law, derive an expression for the electric field at a poi...
Text Solution
|
- निम्न चित्र में विद्युत क्षेत्र अवयव E(x)=alphax^(1//2), E(y)=E(z)=0 ...
Text Solution
|