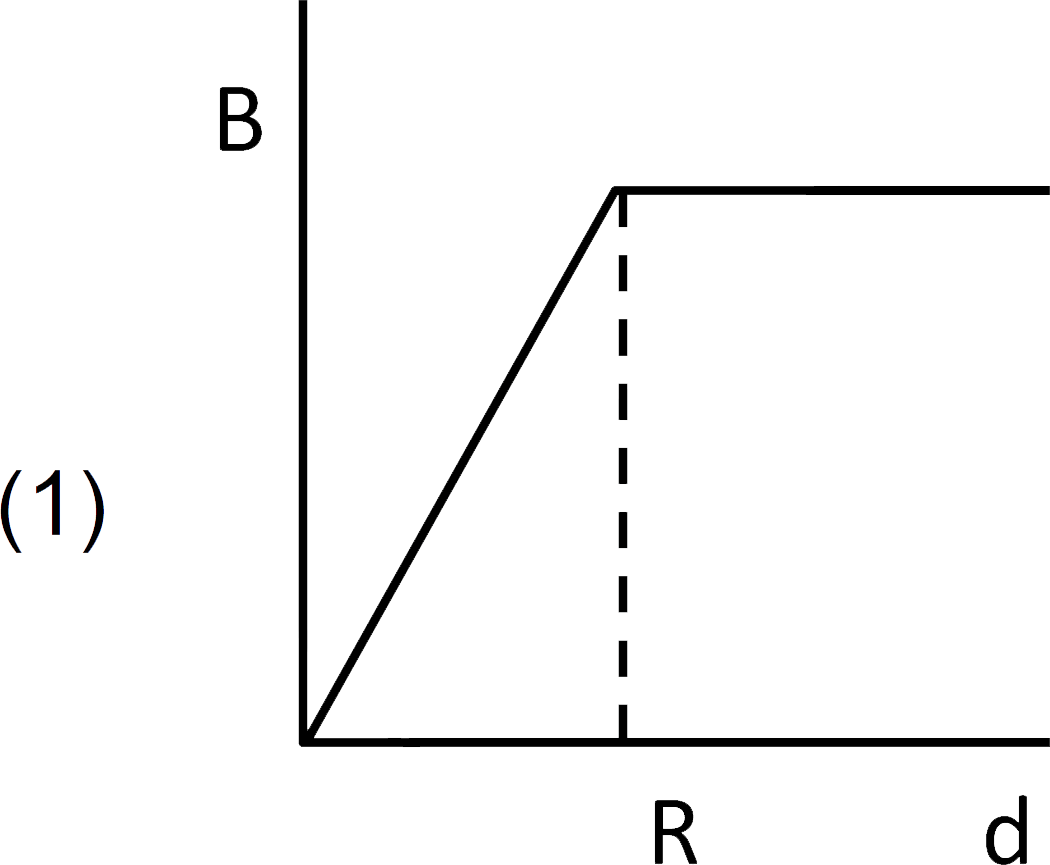
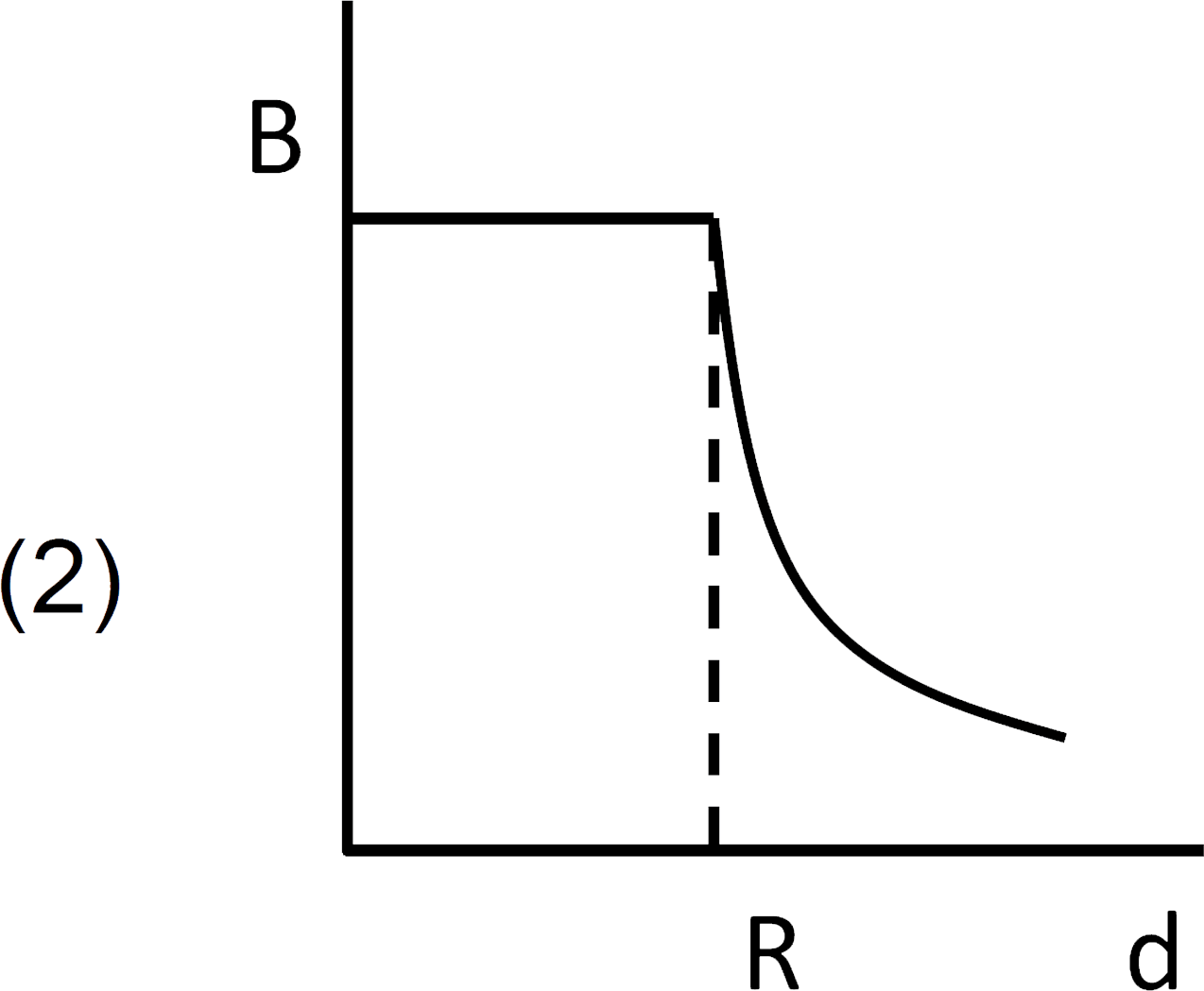
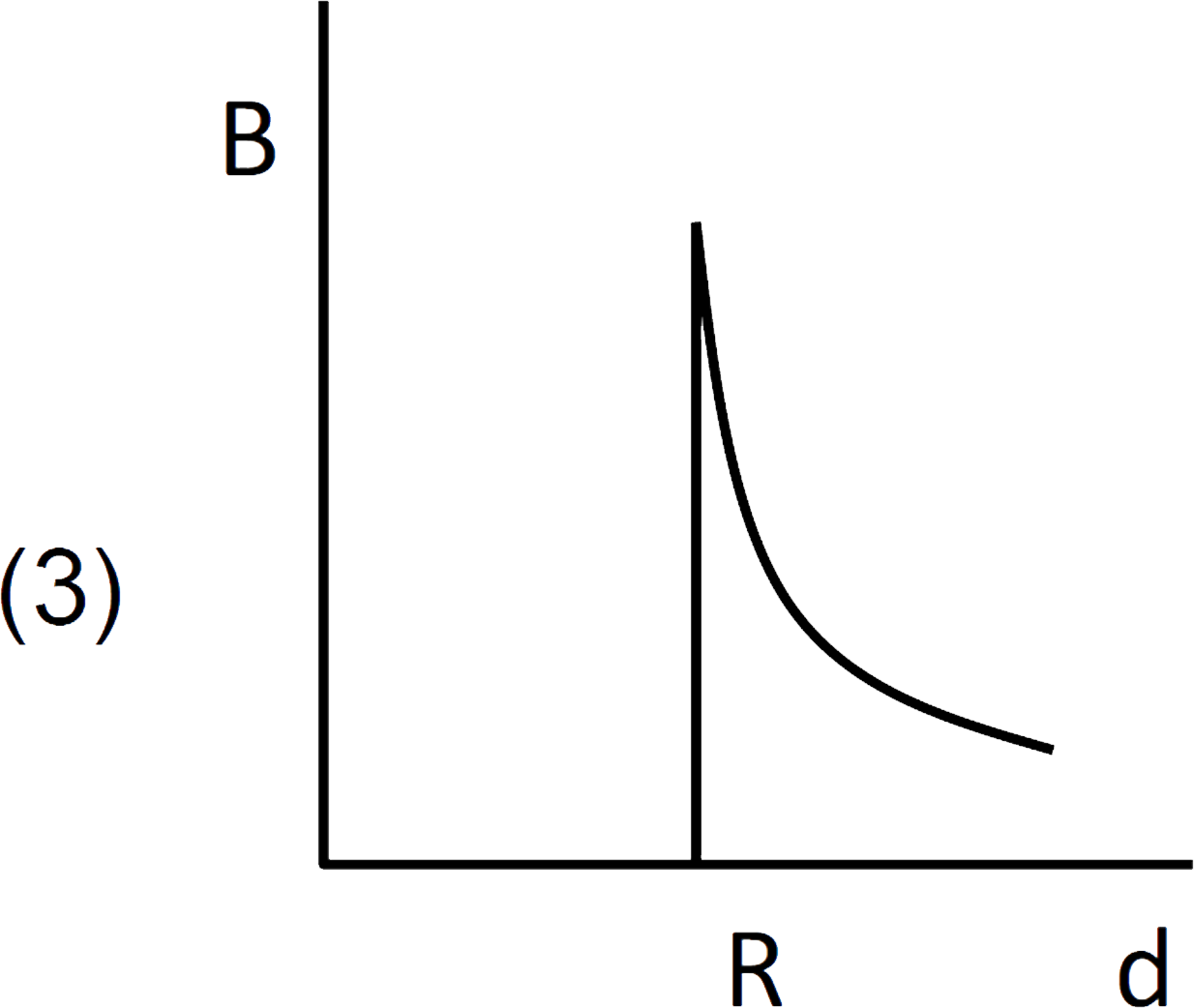
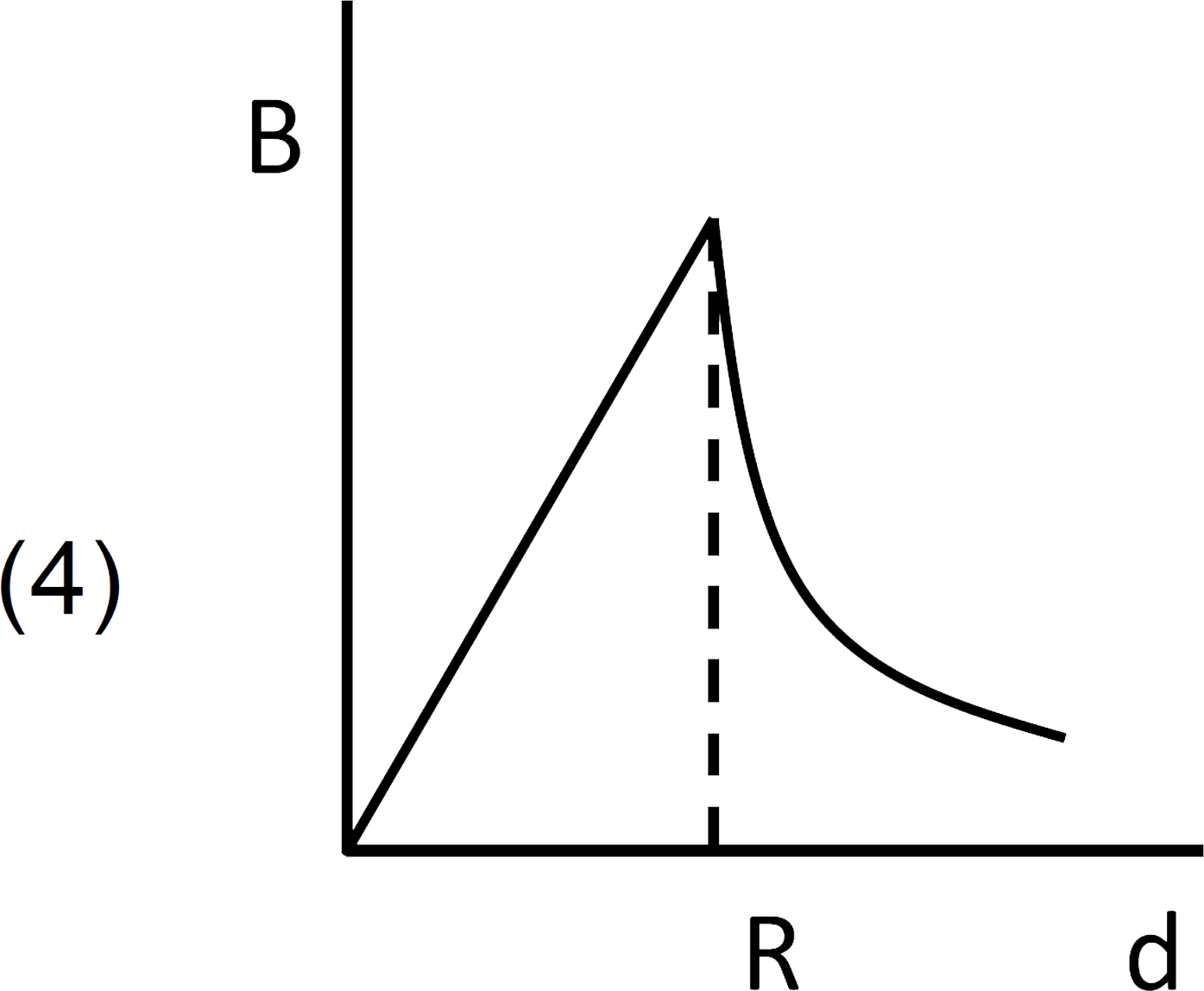
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A cylinderical conductor of radius R is carrying constant current. The...
Text Solution
|
- A cylinderical conductor of radius R is carrying constant current. The...
Text Solution
|
- The magnetic field on the axis of a circular current carrying conducto...
Text Solution
|
- A cylindrical conductor of radius R is carrying a constant current. Th...
Text Solution
|
- The magnetic field produced by a long and straight current carrying co...
Text Solution
|
- The magnetic field at the centre of a circular current carrying conduc...
Text Solution
|
- Which of the graphs shown below correctly represents the variation of ...
Text Solution
|
- A fixed current is flowing from a cylindrical conductor of radius R. W...
Text Solution
|
- The magnetic field B due to a straight conductor of uniform cross-sect...
Text Solution
|