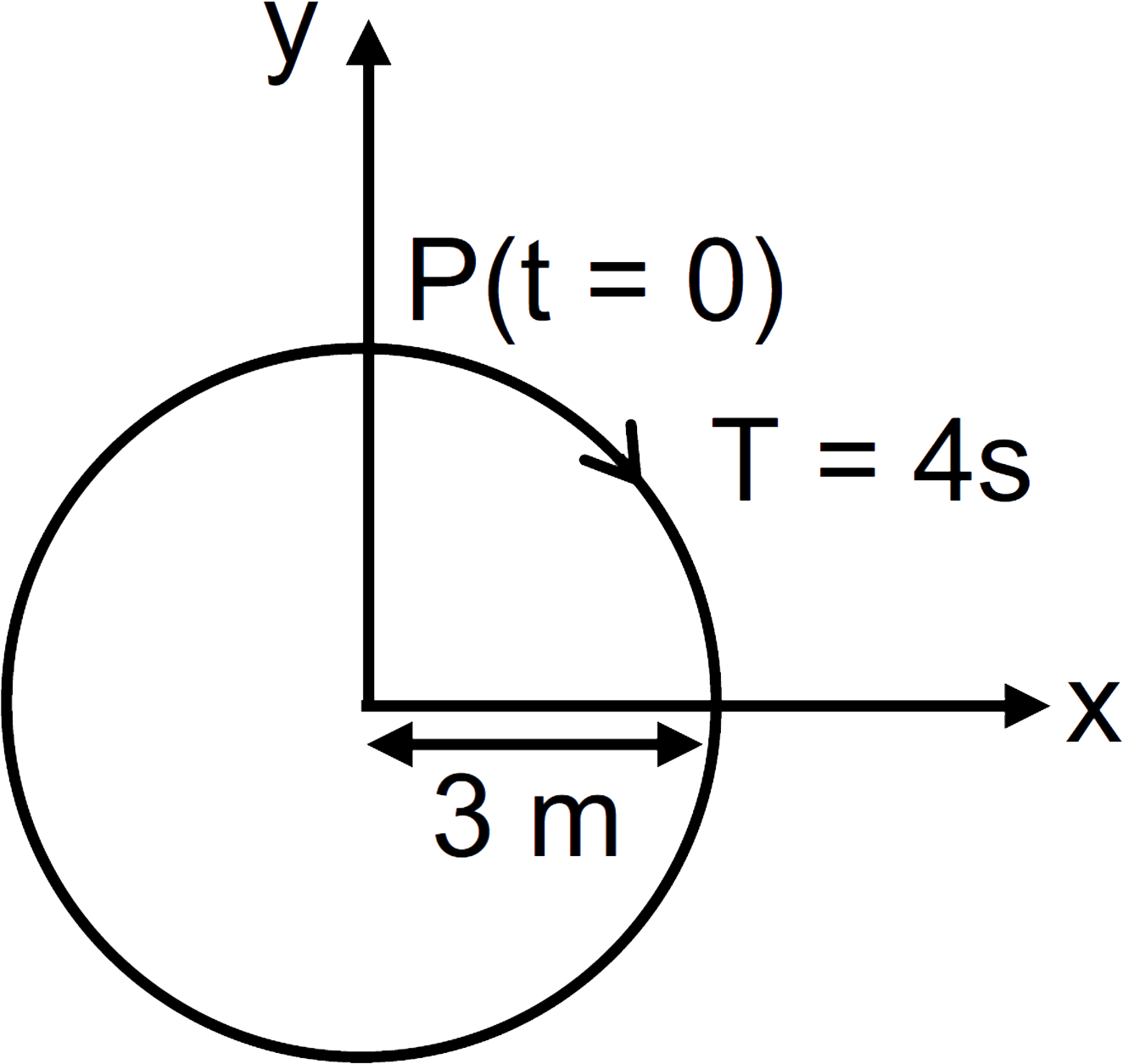A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The radius of cirlcue, the period of revolution, initial position and ...
Text Solution
|
- The radius of cirlcue, the period of revolution, initial position and ...
Text Solution
|
- depict two circulat mothions. The radius of the circle, the period of ...
Text Solution
|
- the circular motion of a particle. The radius of the circle, the perio...
Text Solution
|
- Figure shows the circular motion of a particle. The radius of the circ...
Text Solution
|
- Figure depicts two circular motions. The radius of the circle, the per...
Text Solution
|
- Figure shows the circular motion of a particle. The radius of the circ...
Text Solution
|
- Figure shows the circular motion of a particle. The radius of the circ...
Text Solution
|
- The figure given below depicts two circular motions. The radius of the...
Text Solution
|