A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
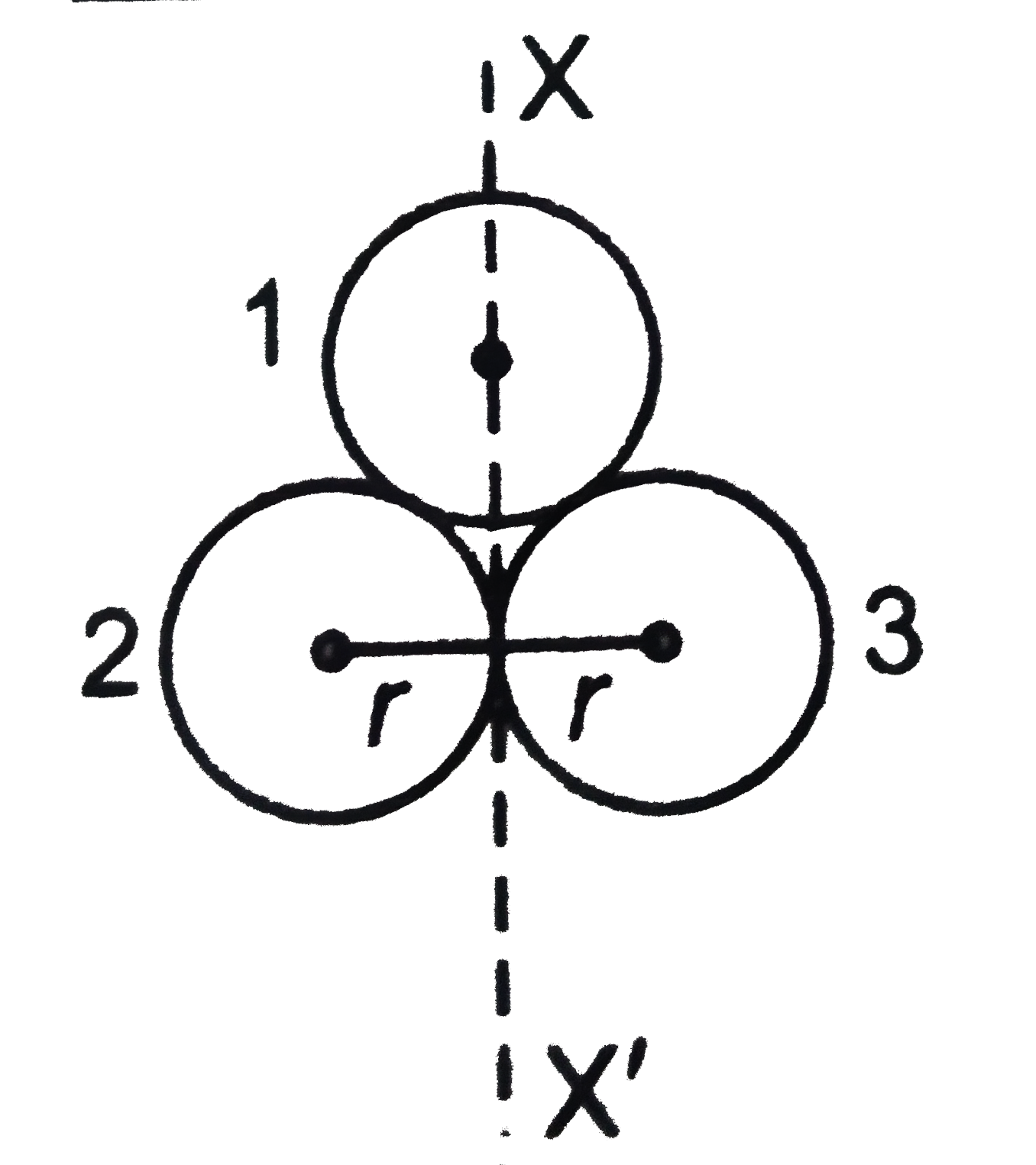
- Three idential spherical shells each of mass m and radius r are placed...
Text Solution
|
- Three idential spherical shells each of mass m and radius r are placed...
Text Solution
|
- गोलीय कोश का व्यास के परितः जड़त्व आघूर्ण होगा:
Text Solution
|
- तीन सर्वसम गोलीय कोशों में प्रत्येक कोशों में प्रत्येक का द्रव्यमान m ...
Text Solution
|
- Three identical spherical shells, each of mass m and radius r are plac...
Text Solution
|
- A spherical shell has a radius of 1.90 m. An applied torque of 960 N-...
Text Solution
|
- A spherical shell has a radius of 1.90 m. An applied torque of 960 N-m...
Text Solution
|
- तीन सर्वसम गोलीय खोखले गोलों में से प्रत्येक का द्रव्यमान m तथा त्रिज्...
Text Solution
|
- Three indentical shperical shells, each of mass m and radius r are pla...
Text Solution
|