A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
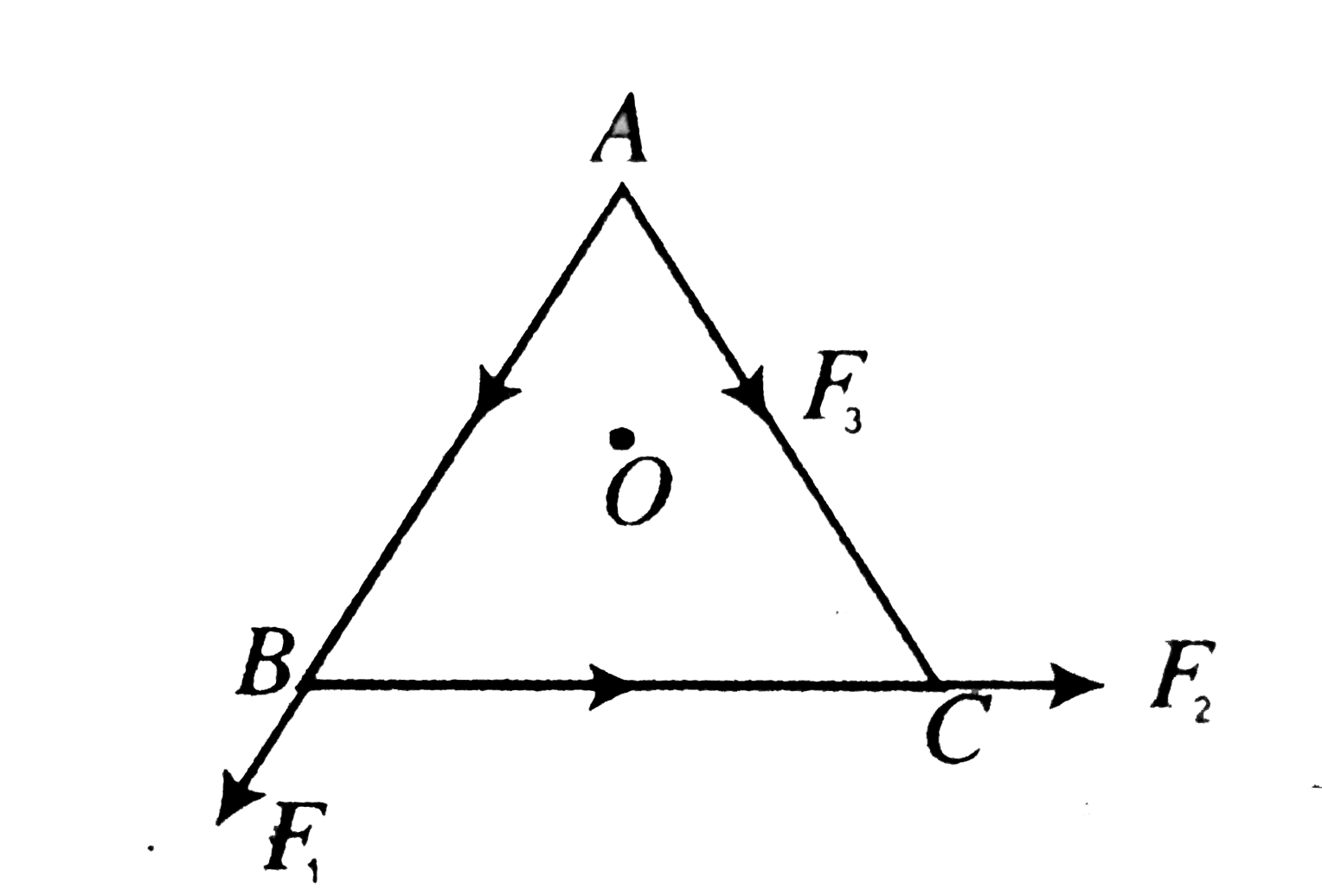
- O is the centre of an equilateral triangle ABC. F(1), F(2) and F(3) ar...
Text Solution
|
- O is the centre of an equilateral triangle ABC. F(1), F(2) and F(3) ar...
Text Solution
|
- When forces F(1) , F(2) , F(3) are acting on a particle of mass m such...
Text Solution
|
- एक समबाहु त्रिभुज ABC का केंद्र O है । F(1),F(2) और F(3) क्रमशः AB...
Text Solution
|
- ABC एक समबाहु त्रिभुज है जिसका केंद्र O है, vec(F(1)), vec(F(2)) तथा v...
Text Solution
|
- ABC is an equilateral with O as its centre vecF(1), vecF(2) and vecF(3...
Text Solution
|
- When three forces F(1), F(2) And F(3) Is acting on an object of mass m...
Text Solution
|
- एक समबाहु त्रिभुज ABC में चित्रानुसार भुजा AB, BC व AC के अनुदिश कार...
Text Solution
|
- When force F(1), F(2), F(3) are acting on a particle of mass m such th...
Text Solution
|